Bất Đẳng Thức Schur

Trong lý thuyết bất đẳng thức, bất đẳng thức Schur, mang tên nhà toán học Đức Issai Schur, là một công cụ quan trọng để giải quyết các bài toán phức tạp liên quan đến ba số thực không âm. Nó không chỉ giúp chứng minh nhiều bất đẳng thức nổi tiếng mà còn đặt nền tảng cho các kỹ thuật và bất đẳng thức mới.

1. Phát biểu

Bất đẳng thức Schur được phát biểu như sau:

Cho \( a, b, c \) là ba số thực không âm và \( r \) là một số thực bất kỳ. Khi đó, bất đẳng thức Schur khẳng định:

a$^r$(a – b)(a – c) + b$^r$(b – c)(b – a) + c$^r$(c – a)(c – b) ≥ 0.

 Trường hợp đặc biệt:

• Khi \( r = 1 \), bất đẳng thức Schur trở thành: a(a – b)(a – c) + b(b – c)(b – a) + c(c – a)(c – b) ≥ 0
• Đây là dạng phổ biến nhất của bất đẳng thức Schur, thường được sử dụng trong các bài toán bất đẳng thức cơ bản.

Điều kiện áp dụng: Bất đẳng thức Schur áp dụng cho \( a, b, c \geq 0 \), và nó đặc biệt mạnh khi \( a, b, c \) có sự bất đối xứng (không bằng nhau).

2. Ý nghĩa của bất đẳng thức Schur

Bất đẳng thức Schur được sử dụng để giải quyết các bài toán bất đẳng thức liên quan đến ba biến. Ý nghĩa chính của bất đẳng thức này bao gồm:

• So sánh giữa ba số thực: Schur cung cấp mối quan hệ giữa các số \( a, b, c \), đặc biệt khi chúng có sự bất đối xứng.
• Chứng minh các bất đẳng thức nổi tiếng khác: Bất đẳng thức Schur thường được sử dụng để chứng minh các bất đẳng thức kinh điển, chẳng hạn như bất đẳng thức Nesbitt, AM-GM (trung bình cộng – trung bình nhân), hay bất đẳng thức Muirhead.
• Tăng cường độ mạnh của bất đẳng thức: Khi áp dụng bất đẳng thức Schur, ta có thể so sánh và đánh giá các biểu thức phức tạp hơn.

3. Chứng minh bất đẳng thức Schur

3.1. Chứng minh với \( r = 1 \)

Xét \( a, b, c \geq 0 \). Biểu thức cần chứng minh là:

S = a(a – b)(a – c) + b(b – c)(b – a) + c(c – a)(c – b) ≥ 0

Bước 1: Sắp xếp các số \( a, b, c \)

Giả sử \( a \geq b \geq c \). Khi đó:

• \( a – b \geq 0 \),
• \( b – c \geq 0 \),
• \( a – c \geq 0 \).

Bước 2: Phân tích từng hạng tử

Xét biểu thức \( S \): $S = (a – b)(a – c)a + (b – c)(b – a)b + (c – a)(c – b)c.$

Do \( a – b \geq 0 \), \( b – c \geq 0 \), và \( a – c \geq 0 \), các hạng tử trong \( S \) sẽ có tính chất bù trừ, đảm bảo tổng \( S \geq 0 \).

Bước 3: Xét các trường hợp đặc biệt

• Nếu \( a = b = c \): \( S = 0 \), bất đẳng thức đúng.
• Nếu \( a > b = c \): \( S = a(a – b)^2 \geq 0 \), bất đẳng thức đúng.
• Nếu \( a = b > c \): \( S = c(c – a)^2 \geq 0 \), bất đẳng thức đúng.

Từ đó, bất đẳng thức được chứng minh.

3.2. Chứng minh tổng quát với \( r > 1 \)

Với \( r > 1 \), bất đẳng thức Schur vẫn đúng nhờ vào tính chất đối xứng của các số \( a, b, c \) và sự ảnh hưởng của hàm mũ \( a^r, b^r, c^r \). Tuy nhiên, chứng minh tổng quát yêu cầu sử dụng kỹ thuật nâng cao như bất đẳng thức Jensen hoặc quy nạp.

4. Các ứng dụng của bất đẳng thức Schur

4.1. Chứng minh bất đẳng thức Nesbitt

Bất đẳng thức Nesbitt khẳng định: $\frac{a}{b+c} + \frac{b}{c+a} + \frac{c}{a+b} \geq \frac{3}{2},$ với \( a, b, c > 0 \).

Chứng minh:

Bất đẳng thức Nesbitt có thể được chứng minh bằng cách sử dụng bất đẳng thức Schur và phương pháp chuẩn hóa.

4.2. Chứng minh bất đẳng thức AM-GM

Bất đẳng thức trung bình cộng – trung bình nhân (AM-GM) khẳng định: $\frac{a+b+c}{3} \geq \sqrt[3]{abc}.$

Chứng minh:

Sử dụng bất đẳng thức Schur kết hợp với các tính chất của hàm lồi, ta dễ dàng chứng minh bất đẳng thức AM-GM.

5. ví dụ minh họa

Ví dụ 1: Chứng minh bất đẳng thức cơ bản

Cho \( a, b, c \geq 0 \). Chứng minh rằng: a(a – b)(a – c) + b(b – c)(b – a) + c(c – a)(c – b) ≥ 0

Giải

– Giả sử \( a \geq b \geq c \). Khi đó, các hiệu \( a – b, b – c, a – c \) đều không âm.

– Áp dụng bất đẳng thức Schur, ta có: S = a(a – b)(a – c) + b(b – c)(b – a) + c(c – a)(c – b) ≥ 0

Do đó, bất đẳng thức được chứng minh.

Ví dụ 2: Bất đẳng thức với hàm mũ

Cho \( a, b, c \geq 0 \). Chứng minh rằng: $a^2(a – b)(a – c) + b^2(b – c)(b – a) + c^2(c – a)(c – b) \geq 0. $

Giải

– Áp dụng bất đẳng thức Schur với \( r = 2 \), ta có: $S = a^2(a – b)(a – c) + b^2(b – c)(b – a) + c^2(c – a)(c – b) \geq 0.$

Ví dụ 3: Cho a,b,c là các số thực không âm.Chứng minh rằng:

$\sqrt{\frac{(a+b)^3}{8ab(4a+4b+c)}}+\sqrt{\frac{(b+c)^3}{8bc(4b+4c+a)}}+\sqrt{\frac{(c+a)^3}{8ca(4c+4a+b)}}\geq 1$

Lời giải

Đặt $P=\sqrt{\frac{(a+b)^3}{8ab(4a+4b+c)}}+\sqrt{\frac{(b+c)^3}{8bc(4b+4c+a)}}+\sqrt{\frac{(c+a)^3}{8ca(4c+4a+b)}}$

$Q=8ab(4a+4b+c)+8bc(4b+4c+a)+8ca(4c+4a+b)$

$=\sum 32ab(a+b)+24abc$

$=32(a+b+c)(ab+bc+ca)-72abc$

Áp dụng BĐT Holder,ta có:

$P^2.Q\geq 8(a+b+c)^3$

Ta cần chứng minh:

$8(a+b+c)^3\geq Q\Leftrightarrow8(a+b+c)^3\geq 32(a+b+c)(ab+bc+ca)-72abc$

$\Leftrightarrow (a+b+c)^3\geq 4(a+b+c)(ab+bc+ca)-9abc$(đúng theo BDT Schur)

Vậy ta có đpcm.

Ví dụ 4: APMO 2004: Cho 3 số thực dương $a,b,c$.Chứng minh rằng:

$(a^2+2)(b^2+2)(c^2+2)\geq 9(ab+bc+ca)$

Lời giải

Lời giải 1: Khai triển bất đẳng thức trên,ta cần chứng minh:

${a^2}{b^2}{c^2} + 2({a^2}{b^2} + {b^2}{c^2} + {c^2}{a^2}) + 4({a^2} + {b^2} + {c^2}) + 8 \ge 9(ab + bc + ca)$

Ta có:$i.a^2+b^2+c^2\geq ab+bc+ca$

$ii.(a^2b^2+1)+(b^2c^2+1)+(c^2a^2+1)\geq 2(ab+bc+ca)$

$iii.a^2b^2c^2+1+1\geq 3\sqrt[3]{a^2b^2c^2}\geq \frac{9abc}{a+b+c}\geq 4(ab+bc+ca)-(a+b+c)^2$ (theo BDT Schur)

Áp dụng các BDT trên,ta có:

$({a^2}{b^2}{c^2} + 2)$ $ + 2({a^2}{b^2} + {b^2}{c^2} + {c^2}{a^2} + 3)$ $ + 4({a^2} + {b^2} + {c^2})$ $ \ge $ 2(ab + bc + ca) + 4(ab + bc + ca) $ + 3({a^2} + {b^2} + {c^2})$ $ \ge 9(ab + bc + ca)(dpcm)$

Lời giải 2: Sử dụng bất đẳng thức AM-GM,ta có:

$(a^2+2)(b^2+2)(c^2+2)-9(ab+bc+ca)$

$=4(a^2+b^2+c^2)+2((a^2b^2+1)+(b^2c^2+1)+(c^2a^2+1))+(a^2b^2c^2+1)+1-9(ab+bc+ca)$

$\geq 4(a^2+b^2+c^2)+4(ab+bc+ca)+2abc+1-9(ab+bc+ca)$

$\geq a^2+b^2+c^2+2abc+1-2(ab+bc+ca)$

Bất đẳng thức cuối đã rất quen thuộc,ta có đpcm.

Ví dụ 5:  VMO 2002-Trần Nam Dũng

Chứng minh rằng với mọi $a,b,c\geq 0$,ta có: $2(a^2+b^2+c^2)+abc+8\geq 5(a+b+c)$

Lời giải

Sử dụng bất đẳng thức AM-GM,ta có:

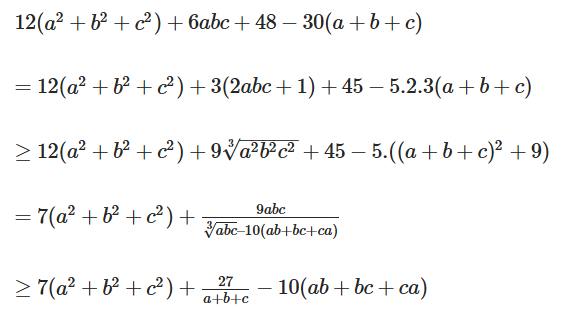
Mặt khác sử dụng bất đẳng thức Schur,

Bất đẳng thức được chứng minh.

Ví dụ 6: Arqady

Cho a,b,c là các số không âm,trong đó không có 2 số nào đồng thời bằng 0.Chứng minh rằng:

$\frac {a}{b^{3} + c^{3}} + \frac {b}{a^{3} + c^{3}} + \frac {c}{a^{3} + b^{3}}\geq\frac {18}{5(a^{2} + b^{2} + c^{2}) – ab – ac – bc}$

Lời giải

Bất đẳng thức cần chứng minh tương đương với

$\sum \frac {a(a + b + c)}{b^3 + c^3} \ge \frac {18(a + b + c)}{5(a^2 + b^2 + c^2) – ab – bc – ca}$

$\Leftrightarrow \sum \frac {a^2}{b^3 + c^3} + \frac {a}{b^2 + c^2 – bc} \ge \frac {18(a + b + c)}{5(a^2 + b^2 + c^2) – ab – bc – ca}$

Áp dụng bất đẳng thức Cauchy-Schwarz,ta có:

$i) \sum \frac {a^2}{b^3 + c^3} \ge \frac {(a^2 + b^2 + c^2)^2}{\sum a^2(b^3 + c^3)}$

$ii) \sum \frac {a}{b^2 + c^2 – bc} \ge \frac {(a + b + c)^2}{\sum a(b^2 + c^2 – bc)}$

Áp dụng 2 bất đẳng thức trên,ta có:

$\frac {(a^2 + b^2 + c^2)^2}{\sum a^2(b^3 + c^3)} + \frac {(a + b + c)^2}{\sum a(b^2 + c^2 – bc)} \ge \frac {18(a + b + c)}{5(a^2 + b^2 + c^2) – ab – bc – ca}$

Giả sử $a + b + c = 1$

Ta cần chứng minh

$\frac {(1 – 2q)^2}{q^2 – (q + 2)r} + \frac {1}{q – 6r} \ge \frac {18}{5 – 11q}$

Bất đẳng thức cuối dễ dàng chứng minh bằng cách xét 2 trường hợp:$1 \ge 4q$ và $4q \ge 1$ 😆

Đẳng thức xảy ra khi $a = b = c$ và $a = b,c = 0$.

Ví dụ 7: Moldova TST 2005: Chứng minh rằng nếu a,b,c là các số thực dương và $a^4+b^4+c^4=3$ thì:

$\frac{1}{4-ab}+\frac{1}{4-bc}+\frac{1}{4-ca}\leq 1$

Lời giải

Quy đồng mẫu số rồi khai triển,ta cần chứng minh:

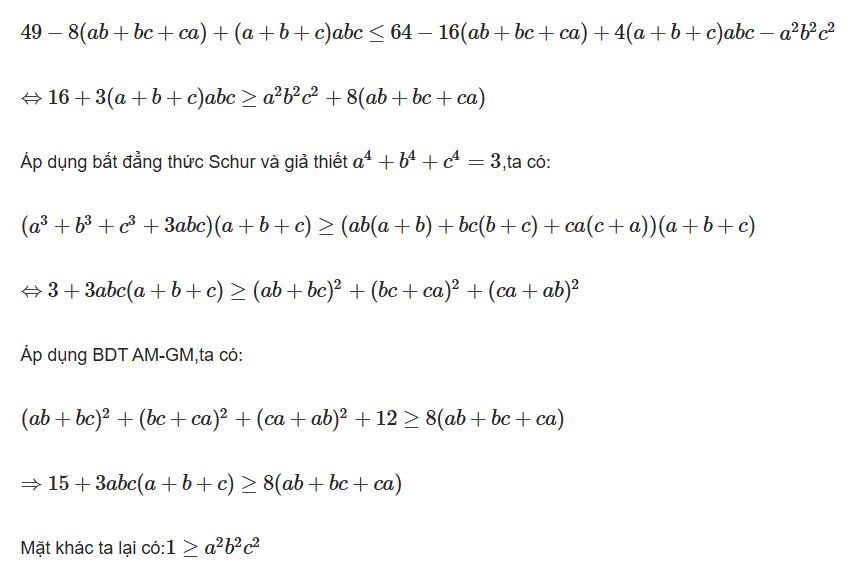
Vậy ta có đpcm.

Ví dụ 8: Vasile Cirtoaje:

Cho $a,b,c$ là các số thực không âm thỏa mãn $ab+bc+ca=3$.Chứng minh rằng:$a^3+b^3+c^3+7abc\geq 10$

Lời giải

Áp dụng BDT Schur,ta có:

$a^3+b^3+c^3+3abc\geq ab(a+b)+bc(b+c)+ca(c+a)$

$\Leftrightarrow a^3+b^3+c^3+6abc\geq (ab+bc+ca)(a+b+c)=pq=3p$

và $r\geq \frac{p(4q-p^2)}{9}=\frac{p(12-p^2)}{9}$

Ta cần chứng minh:

$3p+\frac{p(12-p^2)}{9}\geq 10$

$\Leftrightarrow \frac{(p-3)[(16-p^2)+3(4-p)+2]}{9}\geq 0$

Bất đẳng thức cuối hiển nhiên đúng nên ta có đpcm.

Đẳng thức xảy ra khi $a=b=c=1$.

Ví dụ 9: Võ Thành Văn:

Cho $a,b,c>0,a+b+c=3$.Chứng minh rằng:

$3+\frac{12}{abc}\geq 5(\frac{1}{a}+\frac{1}{b}+\frac{1}{c})$

Lời giải

Đổi biến theo p,q,r,bât đẳng thức cần chứng minh được viết lại như sau:

$3r+12\geq 5q $($\star$)

Mặt khác,theo BDT Schur,ta có:

$3r\geq \frac{3p(4q-p^2)}{9}=4q-9$

$\Rightarrow (\star)\Leftrightarrow 4q-9+12\geq 5q\Leftrightarrow q\le 3(dung)$

Vậy ta có đpcm

Ví dụ 10: Phạm Kim Hùng

Cho a,b,c là các số thực dương thỏa mãn $a^2+b^2+c^2=3$.Chứng minh rằng:

$\frac{1}{2-a}+\frac{1}{2-b}+\frac{1}{2-c}\geq 3$

Lời giải

Quy đồng,rút gọn và đổi biến theo p,q,r, bất đẳng thức cần chứng minh tương đương với $8p+3r\geq 12+5q$

Áp dụng BDT Schur,ta có:

$3r\geq \frac{p(4q-p^2)}{3}=\frac{p(2q-3)}{3}$

Từ giả thiết $p^2-2q=3 \Rightarrow q=\frac{p^2-3}{2}$

Thay 2 điều trên vào bất đẳng thức cần chứng minh,ta có:

$8p+\frac{p(p^2-6)}{3}\geq 12+\frac{5(p^2-3)}{2}$

$\Leftrightarrow (2p-3)(p-3)^2\geq 0$

Bất đẳng thức cuối đúng nên ta có đpcm.

Ví dụ 11: CRUX

Cho a,b,c là các số thực không âm thỏa mãn $a+b+c=3$.Chứng minh rằng:

$\frac{1}{9-ab}+\frac{1}{9-bc}+\frac{1}{9-ca}\le \frac{3}{8}$

* Bài này đã được anh Hùng sử dụng cho phần BDT TRê-bư-sép trong cuốn Sáng tạo BDT,tuy nhiên bây giờ các bạn sẽ được thấy một lời giải với BDT Schur và phương pháp đổi biến p,q,r rất tự nhiên.

Lời giải

Biến đổi bất đẳng thức cần chứng minh và chuyển về dạng $p,q,r$,ta có:

$8(243-18p+3r) \leq 3(729-81q+27r-r^2)$

$\Leftrightarrow 243-99q+57r-3r^2\ge 0$

Theo BDT AM-GM thì $3=3(\frac{a+b+c}{3})^6\geq 3(abc)^2=r^2$

Theo BDT Schur,ta có:

$r\geq \frac{p(4q-p^2)}{3}=\frac{4q-9}{3} \Rightarrow 57r\ge 19(4q-9)$

Nên ta cần chứng minh:

$72-23q-3r^2\ge 0\Leftrightarrow 3(1-r^2)+23(3-q)\ge 0$

Vậy BDT được chứng minh.

Bất đẳng thức Schur là công cụ mạnh mẽ trong bất đẳng thức đại số, giúp xử lý bài toán bất đối xứng và chứng minh nhiều kết quả quan trọng. Hiểu và vận dụng Schur không chỉ giải quyết bài toán phức tạp mà còn rèn luyện tư duy logic và phân tích.