Bất đẳng thức Minkowski là một trong những bất đẳng thức quan trọng nhất trong toán học hiện đại, được đặt theo tên nhà toán học người Đức Hermann Minkowski. Bất đẳng thức này là sự mở rộng của bất đẳng thức tam giác trong hình học Euclid, nhưng được phát triển trong không gian nhiều chiều với các chuẩn tổng quát. Bất đẳng thức này không chỉ là một công cụ mạnh mẽ trong đại số tuyến tính và giải tích mà còn có ứng dụng rộng rãi trong lý thuyết hàm, xác suất, thống kê, và thậm chí cả trong vật lý.

Trong bài viết này, chúng ta sẽ khám phá chi tiết về bất đẳng thức Minkowski, từ định nghĩa, chứng minh, các ví dụ minh họa, đến những ứng dụng thực tiễn trong toán học và các lĩnh vực liên quan.
I. Định nghĩa
Trong không gian Euclid \(n\)-chiều (\(\mathbb{R}^n\)) với chuẩn \(p\) (\(p \geq 1\)).
Cho hai vector \(x = (x_1, x_2, \dots, x_n)\) và \(y = (y_1, y_2, \dots, y_n)\) trong không gian \(\mathbb{R}^n\). Khi đó, bất đẳng thức Minkowski phát biểu như sau:
$ \|x + y\|_p \leq \|x\|_p + \|y\|_p, $ với chuẩn \(p\)-norm được định nghĩa là: $ \|x\|_p = \left( \sum_{i=1}^n |x_i|^p \right)^{\frac{1}{p}}. $
Ý nghĩa: Bất đẳng thức Minkowski là một sự mở rộng của bất đẳng thức tam giác. Trong không gian Euclid 2 chiều hoặc 3 chiều, bất đẳng thức tam giác khẳng định rằng tổng độ dài hai cạnh của một tam giác luôn lớn hơn hoặc bằng độ dài cạnh thứ ba. Trong không gian \(n\)-chiều và với các chuẩn tổng quát, bất đẳng thức này khẳng định điều tương tự cho các vector.
Nếu \(p = 2\), bất đẳng thức Minkowski trở thành bất đẳng thức tam giác trong không gian Euclid với chuẩn phổ biến \(\|x\|_2 = \sqrt{\sum_{i=1}^n x_i^2}\).
II. Chuẩn \(p\) và các trường hợp đặc biệt
Trước khi đi sâu vào chứng minh bất đẳng thức Minkowski, hãy làm rõ ý nghĩa của chuẩn \(p\) và các trường hợp đặc biệt.
Chuẩn \(p\)
Chuẩn \(p\) là một cách đo độ dài hoặc khoảng cách của vector trong không gian \(\mathbb{R}^n\). Với \(p \geq 1\), chuẩn \(p\) được định nghĩa là:
$ \|x\|_p = \left( \sum_{i=1}^n |x_i|^p \right)^{\frac{1}{p}}. $
Một số trường hợp đặc biệt:
- Khi \(p = 1\): Chuẩn \(p\) trở thành tổng giá trị tuyệt đối:$\|x\|_1 = \sum_{i=1}^n |x_i|.$
- Khi \(p = 2\): Chuẩn \(p\) là chuẩn Euclid:$\|x\|_2 = \sqrt{\sum_{i=1}^n x_i^2}.$
- Khi \(p \to \infty\): Chuẩn \(p\) trở thành giá trị lớn nhất trong các thành phần của vector:$\|x\|_\infty = \max_{1 \leq i \leq n} |x_i|.$
Tính chất của chuẩn \(p\)
- \(\|x\|_p \geq 0\), và \(\|x\|_p = 0\) khi và chỉ khi \(x = 0\).
- Tính đồng bậc: \(\|\alpha x\|_p = |\alpha| \|x\|_p\), với mọi \(\alpha \in \mathbb{R}\).
- Bất đẳng thức tam giác tổng quát: \(\|x + y\|_p \leq \|x\|_p + \|y\|_p\).
III. Chứng minh bất đẳng thức Minkowski
Cách 1: Dùng bất đẳng thức Jensen
Cho hai dãy số ${a_1},\,{a_2},\,…,\,{a_n}$ và ${b_1},\,{b_2},\,…,\,{b_n}$ thỏa mãn ${a_i} > 0,\,{b_i} > 0,\,i = \overline {1,\,n} $
Chứng minh rằng $\sqrt[n]{{{a_1}{a_2}…{a_n}}} + \sqrt[n]{{{b_1}{b_2}…{b_n}}} \le \sqrt[n]{{\left( {{a_1} + {b_1}} \right)\left( {{a_2} + {b_2}} \right) + … + \left( {{a_n} + {b_n}} \right)}}$
Chứng Minh
Xét hàm số f(x) = ln(1 + ex)
ta có $f’\left( x \right) = \frac{{{e^x}}}{{1 + {e^x}}} > 0$ với mọi x ∈ R
Suy ra f(x) là hàm lồi trên R.
Áp dụng bất đẳng thức Jensen với ${x_i} = \ln \left( {\frac{{{b_i}}}{{{a_i}}}} \right):$
$\ln \left( {1 + {e^{\frac{{\ln \left( {\frac{{{b_1}}}{{{a_1}}}} \right) + \ln \left( {\frac{{{b_2}}}{{{a_2}}}} \right) + … + \ln \left( {\frac{{{b_n}}}{{{a_n}}}} \right)}}{n}}}} \right) \le \frac{{\ln \left( {\frac{{{b_1}}}{{{a_1}}}} \right) + \ln \left( {\frac{{{b_2}}}{{{a_2}}}} \right) + … + \ln \left( {\frac{{{b_n}}}{{{a_n}}}} \right)}}{n}$
Suy ra: $\ln \left( {1 + \sqrt[n]{{\frac{{{b_1}}}{{{a_1}}}.\frac{{{b_2}}}{{{a_2}}}…\frac{{{b_n}}}{{{a_n}}}}}} \right) \le \ln \left( {\sqrt[n]{{\frac{{\left( {{a_1} + {b_1}} \right).\left( {{a_2} + {b_2}} \right)…\left( {{a_n} + {b_n}} \right)}}{{{a_1}.{a_2}….{a_n}}}}}} \right)$
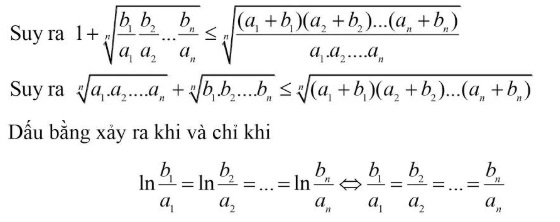
Suy ra điều phải chứng minh.
Cách 2: Dùng bất đẳng thức Hölder
Ý tưởng chứng minh
Bất đẳng thức Minkowski được chứng minh dựa trên bất đẳng thức Hölder – một trong những bất đẳng thức quan trọng khác trong toán học. Trước tiên, hãy nhắc lại bất đẳng thức Hölder:
$\sum_{i=1}^n |a_i b_i| \leq \left( \sum_{i=1}^n |a_i|^p \right)^{\frac{1}{p}} \cdot \left( \sum_{i=1}^n |b_i|^q \right)^{\frac{1}{q}},$
với \(p > 1\), \(q > 1\), và \(\frac{1}{p} + \frac{1}{q} = 1\).
Các bước chứng minh
1. Biểu diễn chuẩn \(p\)
Xét chuẩn \(p\)-norm của \(x + y\): $\|x + y\|_p^p = \sum_{i=1}^n |x_i + y_i|^p.$
2. Áp dụng bất đẳng thức tam giác
Sử dụng tính chất của giá trị tuyệt đối: $ |x_i + y_i|^p \leq \left( |x_i| + |y_i| \right)^p. $
3. Mở rộng lũy thừa \(p\):
Sử dụng định lý khai triển Newton:$ \left( |x_i| + |y_i| \right)^p = |x_i|^p + |y_i|^p + p|x_i|^{p-1}|y_i| + \dots. $
4. Áp dụng bất đẳng thức Hölder:*
Sau khi áp dụng bất đẳng thức Hölder cho các thành phần, ta thu được: $ \sum_{i=1}^n |x_i + y_i|^p \leq \left( \|x\|_p + \|y\|_p \right)^p. $
5. Kết luận
Lấy căn bậc \(p\) hai vế, ta có: $ \|x + y\|_p \leq \|x\|_p + \|y\|_p. $
IV. Phân dạng bài tập
Dạng 1: Vận dụng giải phương trình
Bài tập 1. Giải phương trình $\sqrt {{x^2} + 12x + 61} + \sqrt {{x^2} – 14x + 113} = \sqrt {338} $
Lời giải
Điều kiện xác định:

Bài tập 2. Giải phương trình sau $\sqrt {8{x^2} – 16x + 10} + \sqrt {2{x^2} – 4x + 4} = \sqrt {7 – {x^2} + 2x} $
Lời giải
Điều kiện xác định:

Dạng 2: Vận dụng giải phương trình
Bài tập 1. Giải hệ phương trình $\left\{ \begin{array}{l} {x^2} + xy + {y^2} = 12\\ \sqrt {{x^2} – x + 1} + \sqrt {{y^2} – y + 1} = 2\sqrt 3 \end{array} \right.$
Lời giải
Áp dụng BĐT Minkowski:
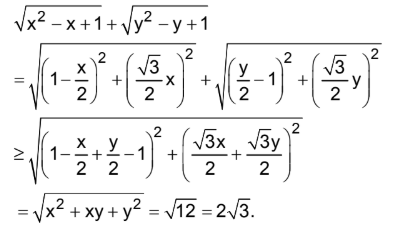
Đẳng thức xảy ra khi x = y = 2.
Vậy nghiệm của hệ là (x; y) = (2; 2)
Bài tập 2. Giải hệ phương trình: $\left\{ \begin{array}{l} \sqrt {{x^2} + {y^2}} + \sqrt {\frac{1}{{{x^2}}} + \frac{1}{{{y^2}}}} = \frac{{5\sqrt 2 }}{2}\\ x – \sqrt {y – 2} = 2 \end{array} \right.$
Lời giải
Điều kiện xác định: x ≥ 2; y ≥ 2;
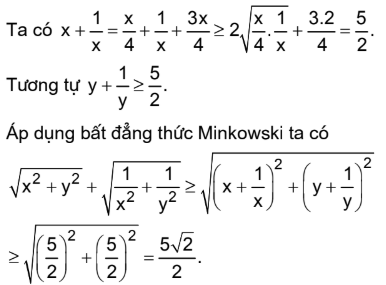
Đẳng thức xảy ra khi x = y = 2
Thay vào phương trình thứ 2 thỏa mãn.
Vậy ta tìm được nghiệm (x; y) = (2; 2)
Dạng 3. Sử dụng để chứng minh bất đẳng thức
Bài tập 1. Cho x, y, z là các số thực dương. Chứng minh rằng $\sqrt {{x^2} – xy + {y^2}} + \sqrt {{y^2} – xz + {z^2}} \ge \sqrt {{z^2} + zx + {x^2}} $
Lời giải
Áp dụng BĐT Minkowski:
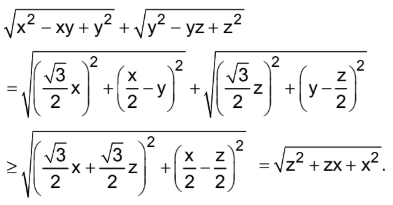
ĐPCM
Bài tập 2. Cho các số thức dương a, b, c thỏa mãn ab + bc + ca = abc. Chứng minh rằng $\frac{{\sqrt {{b^2} + 2{a^2}} }}{{ab}} + \frac{{\sqrt {{c^2} + 2{b^2}} }}{{bc}} + \frac{{\sqrt {{a^2} + 2{c^2}} }}{{ca}} \ge \sqrt 3 $
Lời giải

Dấu bằng xảy ra khi a = b = c = 3.
Bài tập 3. Cho x, y, z là các số thực dương và x + y + z ≤ 1. Hãy chứng minh rằng: $P = \sqrt {{x^2} + \frac{1}{{{x^2}}}} + \sqrt {{y^2} + \frac{1}{{{y^2}}}} + \sqrt {{z^2} + \frac{1}{{{z^2}}}} \ge \sqrt {82} $
Lời giải
Áp dụng bất đẳng thức Minkowski:
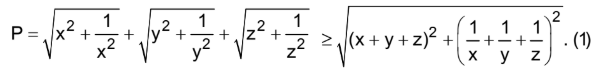
Mặt khác áp dụng BĐT AM-GM:
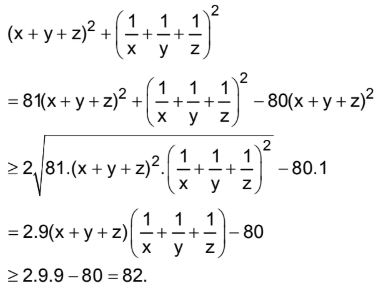
Thay vào (1), ta được
P = \sqrt {{x^2} + \frac{1}{{{x^2}}}} + \sqrt {{y^2} + \frac{1}{{{y^2}}}} + \sqrt {{z^2} + \frac{1}{{{z^2}}}} \ge \sqrt {82} $
Dấu bằng xảy ra khi: x = y = z = 1/3
Dạng 4. Tìm cực trị của một biểu thức đại số
Bài tập 1. Tìm giá trị nhỏ nhất của biểu thức $P = 2\sqrt {9{x^2} – 6x + 2} + 3\sqrt {4{x^2} + 4x + 2} $
Lời giải
Áp dụng BĐT Minkowski:
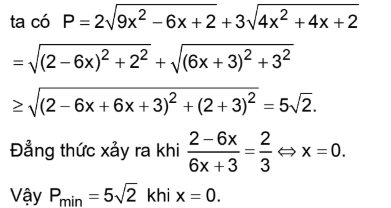
Bài tập 2. Cho a, b, c là các số thực bất kì. Tìm giá trị nhỏ nhất của biểu thức $P = \sqrt {{a^2} + {{\left( {1 – b} \right)}^2}} + \sqrt {{b^2} + {{\left( {1 – c} \right)}^2}} + \sqrt {{c^2} + {{\left( {1 – a} \right)}^2}} $
Lời giải
Áp dụng BĐT Minkowski:
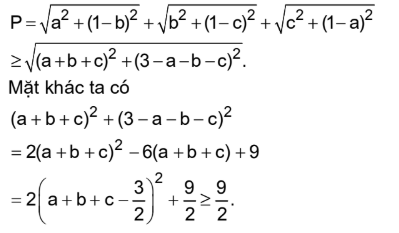
Đẳng thức xảy ra dấu bằng khi a = b = c = 0,5
vậy ${P_{\min }} = \frac{{3\sqrt 2 }}{1}$ khi a = b = c = 0,5
Bài tập 3. Cho a, b là các số thực thỏa mãn (a + 2)(b + 2) = $\frac{{25}}{4}.$ Tìm giá trị nhỏ nhất của biểu thức $F = \sqrt {1 + {a^4}} + \sqrt {1 + {b^4}} $
Lời giải
Theo giả thiết

Bài tập 4. Cho số phức $z=a+bi(a,b\in \mathbb{R})$ thoả mãn $\left| z-4-3i \right|=\left| \overline{z}-2+i \right|.$ Tính giá trị biểu thức $P={{a}^{2}}+{{b}^{2}}$ khi $\left| z+1-3i \right|+\left| z-1+i \right|$ đạt giá trị nhỏ nhất.
Lời giải
Từ giả thiết ta có:
(a – 4)2 + (b – 3)2 = (a – 2)2 + (1 – b)2
⇔ b = 5 – a.
Khi đó:
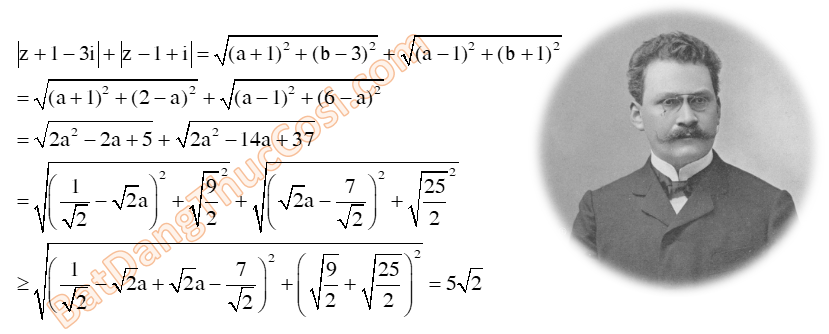
Dấu bằng đạt tại: $\frac{{\frac{1}{{\sqrt 2 }} – \sqrt 2 a}}{{\sqrt 2 a – \frac{7}{{\sqrt 2 }}}} = \frac{{\sqrt {\frac{9}{2}} }}{{\sqrt {\frac{{25}}{2}} }}$ $ \Leftrightarrow a = \frac{{13}}{8}$ $ \Rightarrow b = \frac{{27}}{8}$ $ \Rightarrow P = \frac{{{{13}^2} + {{27}^2}}}{8} = \frac{{449}}{{32}}$
Bài tập 5: Không gian 2 chiều với chuẩn Euclid (\(p = 2\))
Cho hai vector \(x = (3, 4)\) và \(y = (1, 2)\). Tính \(\|x + y\|_2\), \(\|x\|_2\), \(\|y\|_2\), và kiểm tra bất đẳng thức Minkowski.
– Tính \(\|x + y\|_2\):$x + y = (3 + 1, 4 + 2) = (4, 6).$
$\|x + y\|_2 = \sqrt{4^2 + 6^2} = \sqrt{16 + 36} = \sqrt{52}.$
– Tính \(\|x\|_2\) và \(\|y\|_2\):$\|x\|_2 = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = 5, \quad \|y\|_2 = \sqrt{1^2 + 2^2} = \sqrt{1 + 4} = \sqrt{5}.$
– Kiểm tra bất đẳng thức:$\|x + y\|_2 \leq \|x\|_2 + \|y\|_2.$
$\sqrt{52} \leq 5 + \sqrt{5}.$
Vì \(\sqrt{52} \approx 7.21\) và \(5 + \sqrt{5} \approx 7.24\), bất đẳng thức được thỏa mãn.
Bài tập 6: Không gian \(p = 1\)
Cho \(x = (2, -1)\) và \(y = (3, 4)\). Tính \(\|x + y\|_1\), \(\|x\|_1\), \(\|y\|_1\).
– Tính \(\|x + y\|_1\):
$x + y = (5, 3), \quad \|x + y\|_1 = |5| + |3| = 8.$
– Tính \(\|x\|_1\) và \(\|y\|_1\): $\|x\|_1 = |2| + |-1| = 3, \quad \|y\|_1 = |3| + |4| = 7.$
– Kiểm tra bất đẳng thức:$\|x + y\|_1 \leq \|x\|_1 + \|y\|_1.$
$8 \leq 3 + 7.$
Bất đẳng thức được thỏa mãn.
V. Ứng dụng
Trong toán học
- Hình học và đại số tuyến tính: Bất đẳng thức này là cơ sở để nghiên cứu các không gian vector, đặc biệt trong không gian normed.
- Tối ưu hóa: Minkowski được sử dụng để thiết lập các ràng buộc trong bài toán tối ưu hóa.
Trong khoa học dữ liệu: Bất đẳng thức Minkowski được dùng để tính khoảng cách giữa các điểm trong không gian đa chiều, như khoảng cách Manhattan (\(p = 1\)) hoặc khoảng cách Euclid (\(p = 2\)).
Trong vật lý: Không gian Minkowski Là mô hình toán học của không gian-thời gian trong thuyết tương đối đặc biệt, với các tính chất được xây dựng dựa trên bất đẳng thức Minkowski.
Xem thêm tài liệu: Tài liệu bất đẳng thức khác
VI. FAQs
1. Bất đẳng thức Minkowski là gì?
Bất đẳng thức Minkowski là một mở rộng của bất đẳng thức tam giác trong không gian vector, được phát biểu như sau: $\left( \sum_{i=1}^{n} |x_i + y_i|^p \right)^{1/p} \leq \left( \sum_{i=1}^{n} |x_i|^p \right)^{1/p} + \left( \sum_{i=1}^{n} |y_i|^p \right)^{1/p}, \quad p \geq 1.$
2. Bất đẳng thức Minkowski áp dụng trong trường hợp nào?
Nó áp dụng khi làm việc với chuẩn $L^p$ trong không gian vector, đặc biệt là trong giải tích, hình học và lý thuyết đo lường.
3. Bất đẳng thức Minkowski có liên hệ gì với bất đẳng thức tam giác?
Đúng vậy, bất đẳng thức Minkowski chính là sự khái quát hóa của bất đẳng thức tam giác khi áp dụng cho chuẩn $L^p$.
4. Điều kiện để bất đẳng thức Minkowski đúng là gì?
Điều kiện là $p \geq 1$ và các phần tử $x_i, y_i$ phải thuộc không gian có tổng mũ $p$ hội tụ.
5. Bất đẳng thức Minkowski trong không gian $L^2$ có dạng gì?
Trong trường hợp $p=2$, ta có: $\sqrt{\sum_{i=1}^{n} (x_i + y_i)^2} \leq \sqrt{\sum_{i=1}^{n} x_i^2} + \sqrt{\sum_{i=1}^{n} y_i^2}.$
6. Ứng dụng của bất đẳng thức Minkowski trong giải tích hàm là gì?
Nó giúp chứng minh rằng không gian $L^p$ với $p \geq 1$ là không gian chuẩn, từ đó xây dựng nền tảng cho nhiều định lý trong giải tích hàm.
7. Bất đẳng thức Minkowski có được áp dụng trong tích phân không?
Có. Phiên bản tích phân của bất đẳng thức Minkowski là: $\left( \int |f(x) + g(x)|^p dx \right)^{1/p} \leq \left( \int |f(x)|^p dx \right)^{1/p} + \left( \int |g(x)|^p dx \right)^{1/p}.$
8. Khi nào xảy ra dấu bằng trong bất đẳng thức Minkowski?
Dấu bằng xảy ra khi và chỉ khi $x_i$ và $y_i$ tỷ lệ với nhau, tức là tồn tại hằng số $k \geq 0$ sao cho $x_i = k y_i$ với mọi $i$.
9. Bất đẳng thức Minkowski có vai trò gì trong đại số tuyến tính?
Nó hỗ trợ trong việc phân tích vector và chuẩn, giúp thiết lập các tính chất cơ bản của không gian normed.
10. Bất đẳng thức Minkowski có liên quan đến bất đẳng thức Hölder không?
Có. Bất đẳng thức Minkowski thường được chứng minh bằng cách sử dụng bất đẳng thức Hölder.
11. Bất đẳng thức Minkowski trong không gian $\mathbb{R}^n$ có ý nghĩa gì?
Nó cho thấy rằng chuẩn $L^p$ trong $\mathbb{R}^n$ thỏa mãn bất đẳng thức tam giác, chứng minh đây là một chuẩn hợp lệ.
12. Công thức tổng quát của bất đẳng thức Minkowski là gì?
Công thức tổng quát trong không gian $L^p$: $| f + g |_p \leq | f |_p + | g |_p.$
13. Bất đẳng thức Minkowski có ứng dụng trong xác suất thống kê không?
Có. Nó được dùng để chứng minh các tính chất chuẩn $L^p$ của biến ngẫu nhiên và trong lý thuyết moment.
14. Bất đẳng thức Minkowski có dùng trong học máy (machine learning) không?
Có. Nó liên quan đến việc đo độ sai số bằng chuẩn $L^p$, chẳng hạn trong hồi quy và tối ưu hóa.
15. So sánh bất đẳng thức Minkowski và bất đẳng thức Cauchy-Schwarz?
Cauchy-Schwarz áp dụng cho tích vô hướng trong $L^2$, trong khi Minkowski là tổng quát hơn cho mọi $p \geq 1$.
16. Bất đẳng thức Minkowski có thể mở rộng cho nhiều hàm cùng lúc không?
Có. Với nhiều hàm $f_1, f_2, \dots, f_m$, ta có: $\left| \sum_{k=1}^{m} f_k \right|p \leq \sum{k=1}^{m} | f_k |_p.$
17. Bất đẳng thức Minkowski có vai trò gì trong phân tích Fourier?
Nó giúp chứng minh tính chất chuẩn của các không gian $L^p$, từ đó hỗ trợ các định lý trong phân tích Fourier.
18. Có ví dụ cụ thể nào để minh họa bất đẳng thức Minkowski không?
Ví dụ với $x=(1,2)$ và $y=(2,3)$, $p=2$: $\sqrt{(1+2)^2 + (2+3)^2} = \sqrt{9 + 25} = \sqrt{34}.$
Trong khi: $\sqrt{1^2+2^2} + \sqrt{2^2+3^2} = \sqrt{5} + \sqrt{13}.$
Ta thấy $\sqrt{34} \leq \sqrt{5} + \sqrt{13}$ đúng.
19. Bất đẳng thức Minkowski có ứng dụng trong xử lý tín hiệu không?
Có. Nó được sử dụng trong phân tích tín hiệu số, đặc biệt khi tính toán chuẩn $L^p$ của tín hiệu.
20. Bất đẳng thức Minkowski có quan hệ gì với hình học metric?
Nó đảm bảo rằng khoảng cách được định nghĩa bởi chuẩn $L^p$ tuân theo bất đẳng thức tam giác, từ đó tạo ra một không gian metric hợp lệ.
VII.. Kết luận
Bất đẳng thức Minkowski là một bất đẳng thức mạnh mẽ, mở rộng ý tưởng về bất đẳng thức tam giác trong không gian Euclid sang các không gian nhiều chiều và các chuẩn tổng quát. Không chỉ là một công cụ quan trọng trong toán học thuần túy, bất đẳng thức này còn có ứng dụng thực tiễn sâu rộng trong các lĩnh vực như khoa học dữ liệu, vật lý, và tối ưu hóa. Hiểu và vận dụng bất đẳng thức Minkowski không chỉ giúp giải quyết các bài toán toán học phức tạp mà còn mở ra cánh cửa khám phá vẻ đẹp toán học trong thế giới thực.