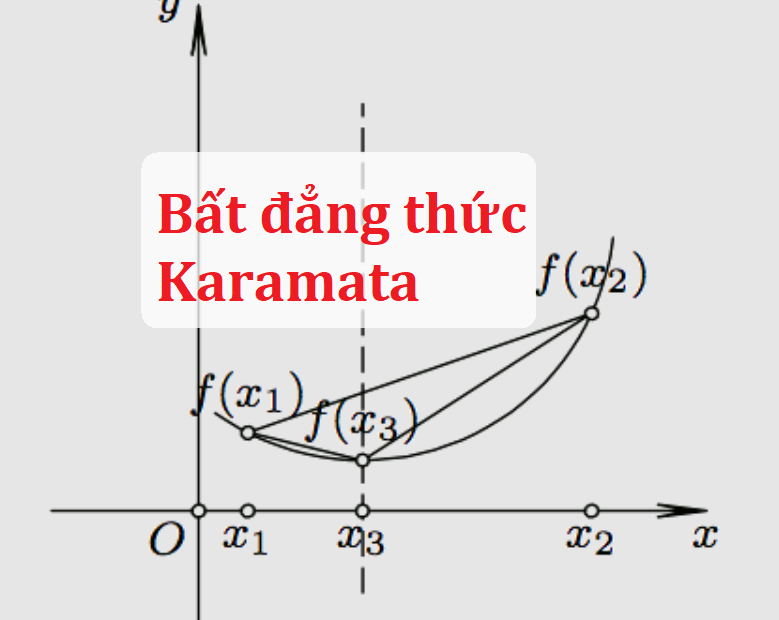
Bất đẳng thức là một chủ đề quan trọng trong toán học, xuất hiện trong đại số, giải tích, hình học và tổ hợp. Trong đó, bất đẳng thức Karamata, do Jovan Karamata đề xuất, là một mở rộng của bất đẳng thức Jensen. Nó là công cụ mạnh mẽ để nghiên cứu hàm lồi, sự bất đối xứng của dãy số và có nhiều ứng dụng trong tối ưu hóa và lý thuyết bất đẳng thức.
1. Phát biểu
Bất đẳng thức Karamataf liên quan đến hàm lồi và hai dãy số thực có tính chất bài toán sắp xếp majorize (hay còn gọi là ưu thế hóa). Phát biểu như sau:
Cho \( f(x) \) là một hàm lồi trên khoảng \( I \), và hai dãy số thực \( a_1, a_2, \dots, a_n \) và \( b_1, b_2, \dots, b_n \) thuộc \( I \), được sắp xếp theo thứ tự giảm dần:
$a_1 \geq a_2 \geq \dots \geq a_n \quad \text{và} \quad b_1 \geq b_2 \geq \dots \geq b_n.$
Nếu: $(a_1, a_2, \dots, a_n) \succeq (b_1, b_2, \dots, b_n),$
nghĩa là \( \mathbf{a} \) majorize \( \mathbf{b} \), thì:
$f(a_1) + f(a_2) + \dots + f(a_n) \geq f(b_1) + f(b_2) + \dots + f(b_n).$
2. Định nghĩa hàm lồi
Hàm \( f(x) \) được gọi là lồi trên một khoảng \( I \) nếu với mọi \( x_1, x_2 \in I \) và \( t \in [0, 1] \), ta có:
$f(tx_1 + (1-t)x_2) \leq tf(x_1) + (1-t)f(x_2).$
Định nghĩa này có nghĩa rằng đồ thị của hàm lồi luôn nằm dưới đoạn thẳng nối hai điểm bất kỳ trên đồ thị.
3. Điều kiện majorize (ưu thế hóa)
Dãy \( \mathbf{a} = (a_1, a_2, \dots, a_n) \) được gọi là majorize dãy \( \mathbf{b} = (b_1, b_2, \dots, b_n) \) nếu:
1. \( a_1 + a_2 + \dots + a_k \geq b_1 + b_2 + \dots + b_k \), với mọi \( k = 1, 2, \dots, n-1 \),
2. \( a_1 + a_2 + \dots + a_n = b_1 + b_2 + \dots + b_n \).
Điều này có nghĩa là tổng của các phần tử đầu tiên trong dãy \( \mathbf{a} \) luôn lớn hơn hoặc bằng tổng tương ứng trong dãy \( \mathbf{b} \), nhưng tổng tất cả các phần tử là như nhau.
4. Chứng minh bất đẳng thức Karamata
Chứng minh bất đẳng thức Karamata dựa trên tính chất của hàm lồi và điều kiện majorize. Dưới đây là ý tưởng chứng minh:
4.1. Sử dụng tính chất của hàm lồi:
– Tính chất của hàm lồi đảm bảo rằng: $f\left(\frac{x + y}{2}\right) \leq \frac{f(x) + f(y)}{2}.$
4.2. Phân tích điều kiện majorize:
– Với điều kiện \( \mathbf{a} \succeq \mathbf{b} \), ta có thể “chuyển hóa” dãy \( \mathbf{a} \) thành \( \mathbf{b} \) bằng cách áp dụng một chuỗi các phép thay thế dạng:
$(x, y) \to \left(\frac{x+y}{2}, \frac{x+y}{2}\right),$
mà không làm thay đổi tổng của các phần tử.
4.3. Áp dụng tính chất hàm lồi:
– Mỗi phép thay thế \( (x, y) \to \left(\frac{x+y}{2}, \frac{x+y}{2}\right) \) làm giảm tổng giá trị hàm \( f \), do \( f(x) \) là lồi.
4.4. Kết luận:
– Sau một chuỗi phép thay thế như vậy, tổng giá trị của \( f(a_1), f(a_2), \dots, f(a_n) \) sẽ lớn hơn hoặc bằng tổng giá trị của \( f(b_1), f(b_2), \dots, f(b_n) \).
Cách khác: Có thể dùng bất đẳng thức Jensen để chứng minh
Một cách phát biểu khác vể bất đẳng thức này:
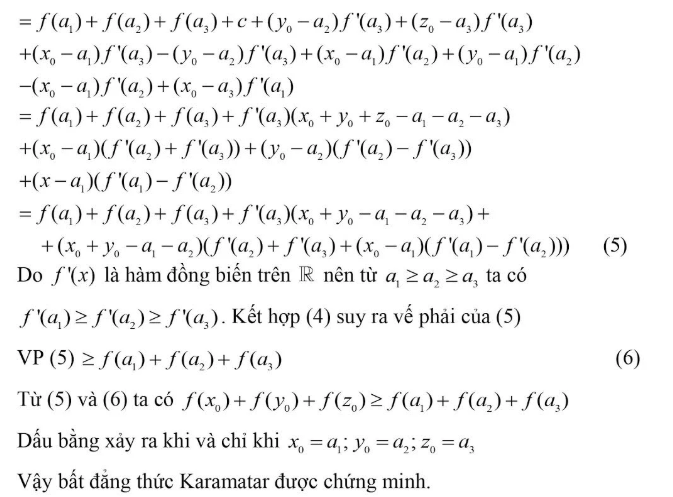
5. Ý nghĩa của bất đẳng thức Karamata
Bất đẳng thức Karamata cho thấy rằng hàm lồi “ưa thích” sự phân phối không cân bằng của các giá trị. Nói cách khác, nếu dãy \( \mathbf{a} \) “tập trung” hơn dãy \( \mathbf{b} \) (theo nghĩa majorize), thì tổng giá trị của hàm lồi trên \( \mathbf{a} \) sẽ lớn hơn hoặc bằng tổng giá trị của hàm lồi trên \( \mathbf{b} \).
6. Ứng dụng của bất đẳng thức Karamata
Chứng minh các bất đẳng thức nổi tiếng
Bất đẳng thức Karamata là một mở rộng của bất đẳng thức Jensen, do đó, nó có thể được sử dụng để chứng minh nhiều bất đẳng thức nổi tiếng, chẳng hạn như:
- Bất đẳng thức AM-GM (Trung bình cộng – Trung bình nhân).
- Bất đẳng thức Chebyshev.
7. Các ví dụ minh họa
Ví dụ 1: Áp dụng bất đẳng thức Karamata
Cho hai dãy \( \mathbf{a} = (4, 2, 1) \) và \( \mathbf{b} = (3, 3, 1) \). Giả sử hàm \( f(x) = x^2 \). Chứng minh rằng:
$f(a_1) + f(a_2) + f(a_3) \geq f(b_1) + f(b_2) + f(b_3).$
Giải
– Dễ thấy \( \mathbf{a} \succeq \mathbf{b} \) vì:
1. \( 4 \geq 3, \quad 4 + 2 \geq 3 + 3, \quad 4 + 2 + 1 = 3 + 3 + 1 \).
2. Tổng của các phần tử \( \mathbf{a} \) và \( \mathbf{b} \) bằng nhau.
– Do \( f(x) = x^2 \) là hàm lồi, ta áp dụng bất đẳng thức Karamata:
$f(4) + f(2) + f(1) \geq f(3) + f(3) + f(1).$
Tính cụ thể:
$4^2 + 2^2 + 1^2 = 16 + 4 + 1 = 21,$
$3^2 + 3^2 + 1^2 = 9 + 9 + 1 = 19.$
Do đó, bất đẳng thức được chứng minh.
Bất đẳng thức Karamata là công cụ quan trọng trong lý thuyết bất đẳng thức, tổng quát hóa nhiều kết quả về hàm lồi và sắp xếp dãy số. Với ứng dụng rộng rãi trong toán học và thực tiễn, nó giúp giải quyết hiệu quả nhiều bài toán phức tạp.