Bất đẳng thức Bunhiacopxki là một quy tắc trong toán học giúp chúng ta so sánh các tổng và tích của các số. Bất đẳng thức này nói rằng, nếu bạn có hai dãy số thực không âm, tổng tích của chúng sẽ không lớn hơn tích của các tổng bình phương của chúng.
1. Bất đẳng thức Bunhiacopski
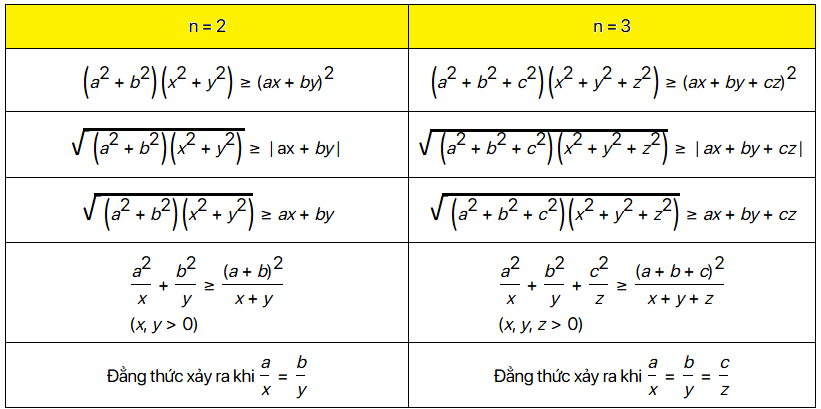
Bất đẳng thức Bunhiacopxki dạng cơ bản
$\left(a^2+b^2\right)\left(c^2+d^2\right) \geq(a c+b d)^2$
Dấu “=” xảy ra khi ac = bd
Bất đẳng thức Bunhiacopxki dạng tổng quát
Với hai bộ số $\left(a_1, a_2, \ldots, a_n\right)$ và $\left(b_1, b_2, \ldots, b_n\right)$, ta có:
$\left(a_1^2+a_2^2+\ldots+a_n^2\right) \cdot\left(b_1^2+b_2^2+\ldots+b_n^2\right) \geq\left(a_1 b_1+a_2 b_2+\ldots+a_n b_n\right)^2$
Dấu “=” xảy ra khi $\frac{a_1}{b_1}=\frac{a_2}{b_2}=\ldots=\frac{a_n}{b_n}$
Nếu một số nào đó (i = 1, 2, 3,…, n) bằng 0 thì đẳng thức tương ứng bằng 0.
2. Chứng minh
Chúng ta có thể chứng minh bất đẳng thức Bunhiacopxki như sau:
$\begin{aligned} & \left(a^2+b^2\right)\left(c^2+d^2\right) \geq(a c+b d)^2 \\ & \Leftrightarrow(a c)^2+(a d)^2+(b c)^2+(b d)^2 \geq(a c)^2+2 a b c d+(b d)^2 \\ & \Leftrightarrow(a d)^2+(b c)^2 \geq 2 a b c d \\ & \Leftrightarrow(a d)^2-2 a b c d+(b c)^2 \geq 0 \\ & \Leftrightarrow(a d-b c)^2 \geq 0 \text { (luôn đúng) }\end{aligned}$
3. Hệ quả quan trọng
Hệ quả 1
Nếu $a_1 x_1+\ldots+a_n x_n=C$ thì $\min \left(x_1^2+\ldots+x_n^2\right)=\frac{C}{a_1^2+\ldots+a_n^2}$ đạt được khi $\frac{x_1}{a_1}=\ldots=\frac{x_n}{a_n}$
Hệ quả 2
Nếu $x_1^2+\ldots+x_n^2=C^2$ (không đổi) thì:
- $\operatorname{Max}\left(a_1 x_1+\ldots+a_n x_n\right)=C \cdot \sqrt{a_1^2+\ldots+a_n^2}$ đạt được khi $a_1 x_1=\ldots=a_n x_n \geq 0$.
- $\operatorname{Min}\left(a_1 x_1+\ldots+a_n x_n\right)=-C \cdot \sqrt{a_1^2+\ldots+a_n^2}$ và dấu “=” xảy ra khi $a_1 x_1=\ldots=a_n x_n \leq 0$
4. Ứng dụng của bất đẳng thức Bunhiacopxki
Bất đẳng thức Bunhiacopxki có nhiều ứng dụng trong toán học, bao gồm:
- Giải bài toán tối ưu: Bất đẳng thức này thường được sử dụng để tìm các giá trị tối ưu trong các bài toán liên quan đến tổng hợp và phân phối.
- Xác định giới hạn: Trong nhiều trường hợp, bất đẳng thức Bunhiacopxki giúp xác định giới hạn cho các biểu thức phức tạp, từ đó giúp rút gọn và phân tích các công thức toán học.
- Chứng minh các bất đẳng thức khác: Nhiều bất đẳng thức nổi tiếng khác, như bất đẳng thức Minkowski và bất đẳng thức AM-GM, có thể được chứng minh bằng cách sử dụng bất đẳng thức Bunhiacopxki.
5. Bài tập vận dụng

Bài tập 1: Chứng minh rằng nếu a, b, c là độ dài ba cạnh của một tam giác có p là nửa chu vi thì $\sqrt{p-a}+\sqrt{p-b}+\sqrt{p-c} \leq \sqrt{3 p}$
Lời giải
Áp dụng bất đẳng thức Bunhiacopxki có:
$\begin{aligned} & \text { 1. } \sqrt{p-a}+1 \cdot \sqrt{p-b}+1 \cdot \sqrt{p-c} \leq \sqrt{\left(1^2+1^2+1^2\right)(p-a+p-b+p-c)} \\ & \Leftrightarrow \sqrt{p-a}+\sqrt{p-b}+\sqrt{p-c} \leq \sqrt{3(3 p-2 p)}=\sqrt{3 p} \text { (điều phải chứng minh) }\end{aligned}$
Dấu “=” xảy ra khi và chỉ khi $\frac{1}{p-a}=\frac{1}{p-b}=\frac{1}{p-c} \Leftrightarrow a=b=c$ hay tam giác là tam giác đều.
Bài tập 2: Cho a, b, c, là số đo 3 cạnh Δ. Chứng minh rằng: $T=\frac{a}{2b+2c-a}+\frac{b}{2c+2a-b}+\frac{c}{2a+2b-c}\geq 1$
Lời giải
Áp dụng bất đăng thức bunhiacopxki cho 6 số:
$\sqrt{\frac{a}{2b+2c-a}}$; $\sqrt{\frac{b}{2c+2a-b}}$; $\sqrt{\frac{c}{2a+2b-c}}$; $\sqrt{\sqrt{a(2b+2c-a)}}$; $\sqrt{\sqrt{b(2c+2a-b)}}$; $\sqrt{\sqrt{c(2a+2b-c)}}$
Ta có: $T.\left [ a(2b+2c-a)+b(2c+2a-b)+c(2a+2b-c) \right ]\geq (a+b+c)^{2}$
Sau đó dùng biến đổi tương đương chứng minh:
$(a+b+c)^{2}\geq 4ab+4bc+4ca-a^{2}-b^{2}-c^{2}$ => đpcm.
Bài tập 3: Cho x > 0; y > 0 và x2 + y2 $\large \leq $ x + y. Chứng minh x + 3y $\large \leq $ 2 + $\large \sqrt{5}$
Lời giải
Giả thiết: x2 + y2 $\large \leq $ x + y
$\large \Leftrightarrow \left ( x-\frac{1}{2} \right )^{2}+\left ( y-\frac{1}{2} \right )^{2}\leq \frac{1}{2}$
Áp dụng bất đẳng thức bunhiacopxki cho 2 bộ số (1;3); $\large \left ( x-\frac{1}{2} ; y-\frac{1}{2}\right )$ ta có:
$\large \left [ 1.\left ( 1-\frac{1}{2} \right )+3.\left ( y-\frac{1}{2} \right ) \right ]^{2}\leq 10\left [ \left ( x-\frac{1}{2} \right )^{2}+\left ( y-\frac{1}{2} \right )^{2} \right ]\leq 5$
$\large \Rightarrow (x+3y-2)^{2}\leq 5$
$\large \Rightarrow x+3y-2\leq \sqrt{5}$
$\large \Rightarrow x+3y\leq 2+\sqrt{5}$
Đẳng thức xảy ra khi $\large \left\{\begin{matrix}
x=\frac{1}{2}+\frac{\sqrt{5}}{10} & \\ y=\frac{1}{2}+\frac{3\sqrt{5}}{10}
\end{matrix}\right.$
Bài tập 4: Tìm giá trị lớn nhất của biểu thức \(A = \sqrt {x – 2} + \sqrt {4 – x}\)
Lời giải
\(A = \sqrt {x – 2} + \sqrt {4 – x}\)
Điều kiện: \(2 \le x \le 4\)
Áp dụng bất đẳng thức Bunhiacopxki có:
\({\left[ {1.\sqrt {x – 2} + 1.\sqrt {4 – x} } \right]^2} \le \left( {{1^2} + {1^2}} \right)\left( {x – 2 + 4 – x} \right) = {2^2} = 4\)
\(\begin{array}{l} \Rightarrow {A^2} \le 4\\ \Leftrightarrow – 2 \le A \le 2 \end{array}\)
A max = 2 khi \(\frac{1}{{\sqrt {x – 2} }} = \frac{1}{{\sqrt {4 – x} }} \Leftrightarrow x – 2 = 4 – x \Leftrightarrow x = 3\)
Vậy max A = 2 khi và chỉ khi x = 3
Bài tập 5: Chứng minh rằng nếu a, b, c là độ dài ba cạnh của một tam giác có p là nửa chu vi thì \(\sqrt {p – a} + \sqrt {p – b} + \sqrt {p – c} \le \sqrt {3p}\)
Lời giải
Áp dụng bất đẳng thức Bunhiacopxki có:
\(1.\sqrt {p – a} + 1.\sqrt {p – b} + 1.\sqrt {p – c} \le \sqrt {\left( {{1^2} + {1^2} + {1^2}} \right)\left( {p – a + p – b + p – c} \right)}\)
\(\Leftrightarrow \sqrt {p – a} + \sqrt {p – b} + \sqrt {p – c} \le \sqrt {3\left( {3p – 2p} \right)} = \sqrt {3p}\)(điều phải chứng minh)
Dấu “=” xảy ra khi và chỉ khi \(\frac{1}{{p – a}} = \frac{1}{{p – b}} = \frac{1}{{p – c}} \Leftrightarrow a = b = c\) hay tam giác là tam giác đều
Bài tập 6: Cho a, b, c là các số thực dương bất kỳ. Chứng minh rằng:
\(\sqrt {\frac{{a + b}}{{a + b + c}}} + \sqrt {\frac{{b + c}}{{a + b + c}}} + \sqrt {\frac{{c + a}}{{a + b + c}}} \le \sqrt 6\)
Lời giải
Áp dụng bất đẳng thức Bunhiacopxki ta có:
\(1.\sqrt {\frac{{a + b}}{{a + b + c}}} + 1.\sqrt {\frac{{b + c}}{{a + b + c}}} + 1.\sqrt {\frac{{c + a}}{{a + b + c}}}\)
\(\le \sqrt {\left( {{1^2} + {1^2} + {1^2}} \right)\left( {\frac{{a + b}}{{a + b + c}} + \frac{{b + c}}{{a + b + c}} + \frac{{c + a}}{{a + b + c}}} \right)}\)
\(\Leftrightarrow \sqrt {\frac{{a + b}}{{a + b + c}}} + \sqrt {\frac{{b + c}}{{a + b + c}}} + \sqrt {\frac{{c + a}}{{a + b + c}}} \le \sqrt {3.2} = \sqrt 6\) (điều phải chứng minh)
Dấu “=” xảy ra khi và chỉ khi a = b = c
Bài tập 7: Chứng minh: $\sqrt{a-1}+\sqrt{b-1}+\sqrt{c-1}\leq \sqrt{c(ab+1)}$ với mọi số thực dương a;b;c $\geq 1$
Lời giải
Đặt a – 1 = x2 ; b – 1 = y2; c – 1 = z2
Với x;y;z > 0. Bất đẳng thức cần chứng minh trở thành:
$x+y+z\leq \sqrt{(z^{2}+1)\left [ (x^{2}+1)(y^{2}+1)+1 \right ]}$
Áp dụng bất đẳng thức bunhiacopxki ta có:
$x+y\leq \sqrt{(x^{2}+1)(y^{2}+1)}\Rightarrow x+y+z\leq \sqrt{(x^{2}+1)(y^{2}+1)}+z(1)$
$ \sqrt{(x^{2}+1)(y^{2}+1)}+z\leq \sqrt{(x^{2}+1)(y^{2}+1)+1}.\sqrt{z^{2}+1}(2)$
Từ (1) và (2) ta có: $ x+y+z\leq \sqrt{(z^{2}+1)\left [ (x^{2}+1)(y^{2}+1)+1 \right ]}$
Vậy $\sqrt{a-1}+\sqrt{b-1}+\sqrt{c-1}\leq \sqrt{c(ab+1)}$ với mọi số thực dương a;b;c $\geq 1$
Bài tập 8: Cho a;b và thỏa mãn a2 + b2 = 9. Chứng minh $ \frac{ab}{a+b+3}\leq \frac{3\sqrt{2}-3}{2}$
Ta có: a2 + b2 = 9
$ \Leftrightarrow 2ab=(a+b)^{2}-9$
$ \Leftrightarrow 2ab=(a+b+3)(a+b-3)$
$ \Leftrightarrow \frac{2ab}{a+b+3}=a+b-3$
$ \Leftrightarrow \frac{ab}{a+b+3}=\frac{a+b}{2}-\frac{3}{2}$
Mà theo bất đẳng thức bunhiacopxki thì $ a+b\leq \sqrt{2}.\sqrt{a^{2}+b^{2}}=3\sqrt{2}$
Nên: $ \frac{ab}{a+b+3}\leq \frac{3\sqrt{2}-3}{2}$
Đẳng thức xảy ra khi: $\left\{\begin{matrix}
a;b>0& & \\ a^{2}+b^{2}=9\Leftrightarrow a=b=\frac{3}{\sqrt{2}}
& & \\a=b
\end{matrix}\right.$
Tài liệu tham khảo:
6. FAQs
FAQs
1. Bất đẳng thức Bunhiacopxki phát biểu như thế nào?
Trả lời: Với hai dãy số thực \(a_1, a_2, \ldots, a_n\) và \(b_1, b_2, \ldots, b_n\), ta có:
$\left( \sum_{i=1}^{n} a_i^2 \right)\left( \sum_{i=1}^{n} b_i^2 \right) \geq \left( \sum_{i=1}^{n} a_i b_i \right)^2$
2. Dấu bằng trong bất đẳng thức Bunhiacopxki xảy ra khi nào?
Trả lời: Dấu bằng xảy ra khi tồn tại hằng số (k) sao cho: $a_i = k b_i \quad \forall i$
3. Bất đẳng thức Bunhiacopxki có tên gọi khác không?
Trả lời: Có, nó còn được gọi là bất đẳng thức Cauchy–Schwarz hoặc Cauchy–Bunyakovsky trong nhiều tài liệu toán học quốc tế.
4. Phiên bản tích phân của bất đẳng thức Bunhiacopxki là gì?
Trả lời: Với các hàm số khả tích \(f(x), g(x)\) trên \([a, b]\), ta có:
$\left( \int_a^b f(x) g(x) , dx \right)^2 \leq \left( \int_a^b f(x)^2 , dx \right)\left( \int_a^b g(x)^2 , dx \right)$
5. Có dạng không gian vectơ của bất đẳng thức Bunhiacopxki không?
Trả lời: Có. Với hai vectơ \( \mathbf{u}, \mathbf{v} \) trong không gian Euclid, ta có:
$|\langle \mathbf{u}, \mathbf{v} \rangle| \leq |\mathbf{u}| \cdot |\mathbf{v}|$
6. Ứng dụng trong chứng minh toán học của bất đẳng thức Bunhiacopxki là gì?
Trả lời: Nó thường được dùng để chứng minh các bất đẳng thức đại số, phân tích, và trong việc thiết lập chuẩn trong không gian vectơ.
7. Bất đẳng thức Bunhiacopxki có liên hệ gì với hình học phẳng?
Trả lời: Nó được dùng để chứng minh các bất đẳng thức về độ dài cạnh, diện tích tam giác và góc trong hình học phẳng.
8. Bất đẳng thức Bunhiacopxki có vai trò gì trong không gian Hilbert?
Trả lời: Đây là bất đẳng thức nền tảng đảm bảo tích vô hướng xác định được chuẩn trong không gian Hilbert.
9. Có thể chứng minh bất đẳng thức Bunhiacopxki bằng phương pháp bình phương không âm không?
Trả lời: Có. Ta xét: $\sum_{i=1}^{n} (a_i – \lambda b_i)^2 \geq 0$
Chọn
$\lambda = \dfrac{\sum a_i b_i}{\sum b_i^2}$
ta thu được bất đẳng thức.
10. Bất đẳng thức Bunhiacopxki có ứng dụng trong xác suất không?
Trả lời: Có. Nó được dùng trong chứng minh bất đẳng thức về hiệp phương sai và phương sai của biến ngẫu nhiên.
11. Bất đẳng thức Bunhiacopxki được áp dụng trong giải tích như thế nào?
Trả lời: Nó được dùng để chứng minh hội tụ của chuỗi, tích phân và thiết lập giới hạn trên cho các biểu thức phức tạp.
12. Bất đẳng thức Bunhiacopxki có áp dụng cho số phức không?
Trả lời: Có. Với \(z_i, w_i \in \mathbb{C}\), ta có: $\left| \sum_{i=1}^n z_i \overline{w_i} \right|^2 \leq \left( \sum_{i=1}^n |z_i|^2 \right)\left( \sum_{i=1}^n |w_i|^2 \right)$
13. Mối quan hệ giữa bất đẳng thức Bunhiacopxki và bất đẳng thức Hölder là gì?
Trả lời: Bunhiacopxki là trường hợp đặc biệt của bất đẳng thức Hölder khi (p = q = 2).
14. Có thể sử dụng bất đẳng thức Bunhiacopxki trong vật lý không?
Trả lời: Có. Nó thường xuất hiện trong cơ học lượng tử, đặc biệt khi phân tích các trạng thái sóng và chuẩn hóa hàm sóng.
15. Ứng dụng của bất đẳng thức Bunhiacopxki trong thi Olympic Toán là gì?
Trả lời: Đây là công cụ cực kỳ phổ biến để xử lý các bài toán chứng minh bất đẳng thức phức tạp ở cấp độ trung học và đại học.
16. Bất đẳng thức Bunhiacopxki có thể minh họa bằng ví dụ đơn giản không?
Trả lời: Với \(a = (1,2), b = (3,4)\):
$(1^2 + 2^2)(3^2 + 4^2) = (5)(25) = 125 \geq (1\cdot 3 + 2\cdot 4)^2 = 11^2 = 121$
Bất đẳng thức đúng.
17. Bất đẳng thức Bunhiacopxki có vai trò trong thống kê không?
Trả lời: Có. Nó dùng để thiết lập giới hạn cho hiệp phương sai và áp dụng trong phân tích dữ liệu.
18. Bất đẳng thức Bunhiacopxki có ứng dụng trong học máy (machine learning) không?
Trả lời: Có. Nó liên quan trực tiếp đến tích vô hướng và chuẩn của vectơ, được dùng trong các thuật toán tối ưu và học sâu.
19. Tại sao bất đẳng thức Bunhiacopxki lại quan trọng trong toán học hiện đại?
Trả lời: Vì nó là nền tảng cho rất nhiều nhánh toán học: giải tích hàm, không gian Hilbert, xác suất, vật lý toán và khoa học dữ liệu.
20. Có tài liệu nào nên tham khảo thêm về bất đẳng thức Bunhiacopxki?
Trả lời: Bạn có thể xem trong các giáo trình Giải tích, Đại số tuyến tính, và các tuyển tập bất đẳng thức toán học của Engel, Hardy–Littlewood–Pólya.