Bất đẳng thức Young, đặt theo tên nhà toán học William Henry Young, là một công cụ quan trọng trong giải tích và lý thuyết bất đẳng thức. Nó có ứng dụng rộng rãi trong toán học thuần túy, tối ưu hóa, phân tích hàm và vật lý. Bất đẳng thức này xuất hiện trong các lý thuyết về tích phân, chuỗi số, không gian Sobolev và nhiều lĩnh vực khác.
1. Phát biểu
1.1. Dạng cơ bản
Bất đẳng thức Young khẳng định rằng, với hai số thực không âm \( a, b \) và hai số thực dương \( p, q \) thỏa mãn \( \frac{1}{p} + \frac{1}{q} = 1 \), ta có:
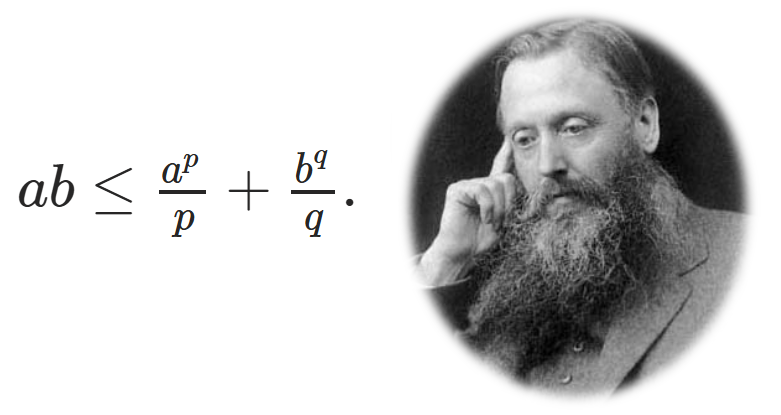
Dấu bằng xảy ra khi \( a^p = b^q \). Điều này có nghĩa là: $a^p / p = b^q / q,$ tức \( a \) và \( b \) đạt được sự cân bằng theo các hằng số \( p \) và \( q \).
1.2. Bất đẳng thức Young tổng quát
Cho hai dãy số \( \{a_i\} \) và \( \{b_i\} \) không âm, với các số mũ \( p_i, q_i > 1 \) thỏa mãn \( \frac{1}{p_i} + \frac{1}{q_i} = 1 \), ta có:
$\sum_{i} a_i b_i \leq \sum_{i} \left( \frac{a_i^{p_i}}{p_i} + \frac{b_i^{q_i}}{q_i} \right)$
Dấu “=” xảy ra khi \( a_i^{p_i} = b_i^{q_i} \) với mọi \( i \).
1.3. Bất đẳng thức Young trong đại số tuyến tính
Cho hai ma trận \( A \) và \( B \) cùng kích thước, với các chuẩn ma trận \( \|A\|_p \) và \( \|B\|_q \) thỏa mãn \( \frac{1}{p} + \frac{1}{q} = 1 \), ta có:
$\|AB\|_1 \leq \frac{\|A\|_p^p}{p} + \frac{\|B\|_q^q}{q}$
2. Ý nghĩa
Bất đẳng thức Young có ý nghĩa quan trọng trong phân tích hàm và giải tích vì nó cho thấy mối tương quan giữa tích của hai số không âm và tổng của các lũy thừa của chúng. Một số ý nghĩa quan trọng bao gồm:
Đánh giá tích của hai số:
Bất đẳng thức Young cung cấp một cách để ước lượng tích \( ab \), đặc biệt khi \( a \) và \( b \) không cân bằng. Nó giới hạn giá trị của \( ab \) bằng tổng của các lũy thừa \( a^p/p \) và \( b^q/q \).
Cân bằng giữa các hạng tử:
Bất đẳng thức giúp tối ưu hóa các bài toán có liên quan đến cân bằng giữa hai biến, chẳng hạn như bài toán xác định một giá trị tối thiểu hoặc tối đa.
Ứng dụng trong các không gian tích phân:
Trong giải tích, bất đẳng thức Young được mở rộng để áp dụng cho các hàm số và tích phân, đặc biệt trong lý thuyết không gian Sobolev và các bài toán phân tích Fourier.
3. Chứng minh
Chuẩn bị
Trước khi chứng minh, chúng ta cần nhắc lại một số tính chất quan trọng:
- Hàm mũ \( x^p \) với \( p > 1 \) là một hàm lồi.
- Tính chất của hàm lồi: Đối với hàm \( f(x) \) lồi, ta có \( f(tx + (1-t)y) \leq tf(x) + (1-t)f(y) \), với \( t \in [0, 1] \).
Chứng minh dạng cơ bản
Cho \( a, b \geq 0 \) và \( \frac{1}{p} + \frac{1}{q} = 1 \). Ta chứng minh bất đẳng thức: $ab \leq \frac{a^p}{p} + \frac{b^q}{q}.$
Bước 1: Sử dụng hàm lồi
Xét hàm \( f(x) = e^x \), ta biết rằng hàm số này là lồi. Theo bất đẳng thức Jensen cho hàm lồi, với \( t = \frac{1}{p} \) và \( 1-t = \frac{1}{q} \), ta có:
$e^{ta + (1-t)b} \leq t e^a + (1-t)e^b.$
Bước 2: Áp dụng vào bất đẳng thức Young
Chọn \( x = \ln a \) và \( y = \ln b \), từ đó: $a^t b^{1-t} \leq t a + (1-t) b.$
Nhân cả hai vế với \( p \cdot q \), từ đó suy ra: $ab \leq \frac{a^p}{p} + \frac{b^q}{q}.$
Cách Khác: Ta có thể dùng bất đẳng thức Jensen để chứng minh bất đẳng thức Young
Bất đẳng thức hiển nhiên đúng khi \( a = 0 \) hoặc \( b = 0 \). Giả sử \( a > 0 \), \( b > 0 \).
Xét hàm số \( f(x) = e^x \) suy ra \( f”(x) = e^x > 0 \) với mọi \( x \in \mathbb{R} \).
Suy ra \( f(x) \) lồi trên \( \mathbb{R} \).
$f\left( \frac{1}{p} \ln a^p + \frac{1}{q} \ln b^q \right) \leq \frac{1}{p} f(\ln a^p) + \frac{1}{q} f(\ln b^q)$
hay
$f(\ln a + \ln b) \leq \frac{1}{p} f(p \ln a) + \frac{1}{q} f(q \ln b)$
hay
$e^{\ln ab} \leq \frac{1}{p} e^{p \ln a} + \frac{1}{q} e^{q \ln b}$
$\Leftrightarrow ab \leq \frac{a^p}{p} + \frac{b^q}{q}$
4. Các dạng mở rộng của Bất Đẳng Thức Young
Bất đẳng thức Young có nhiều dạng mở rộng khác nhau, bao gồm:
4.1. Dạng tích phân
Cho các hàm \( f(x) \) và \( g(x) \) thuộc không gian tích phân \( L^p \) và \( L^q \), với \( \frac{1}{p} + \frac{1}{q} = 1 \), ta có:
$\int_\Omega f(x)g(x) \, dx \leq \frac{\|f\|_p^p}{p} + \frac{\|g\|_q^q}{q}.$
Dấu bằng xảy ra khi \( f \) và \( g \) đạt cân bằng liên quan đến \( p \) và \( q \).
4.2. Dạng bất đẳng thức Holder
Bất đẳng thức Young có liên quan chặt chẽ đến bất đẳng thức Holder:
$\int_\Omega |f(x)g(x)| \, dx \leq \|f\|_p \|g\|_q,$ với \( \frac{1}{p} + \frac{1}{q} = 1 \). Đây thực chất là một cách diễn đạt khác của bất đẳng thức Young.
5. Ứng dụng
5.1. Trong giải tích
Bất đẳng thức Young được sử dụng trong các bài toán liên quan đến tích phân, đặc biệt là trong không gian Sobolev. Ví dụ:
- Phân tích Fourier: Bất đẳng thức Young được áp dụng để ước lượng các chuẩn của chuỗi Fourier.
- Ước lượng tích phân: Giúp đánh giá giá trị của các tích phân khi các hàm số không đều nhau.
5.2. Trong lý thuyết tối ưu hóa
Trong tối ưu hóa, bất đẳng thức Young giúp giải quyết các bài toán cân bằng, chẳng hạn như phân phối tài nguyên hoặc xác định các giá trị tối ưu trong kinh tế học.
5.3. Trong vật lý
Bất đẳng thức Young xuất hiện trong các phép phân tích năng lượng, chẳng hạn như trong cơ học lượng tử hoặc nhiệt động lực học, nơi cần ước lượng các đại lượng vật lý.
5.4. Trong các bài toán bất đẳng thức
Bất đẳng thức Young là công cụ mạnh mẽ để chứng minh các bất đẳng thức nổi tiếng khác, chẳng hạn như bất đẳng thức AM-GM, bất đẳng thức Holder, và bất đẳng thức Minkowski.
6. Ví dụ minh họa
Ví dụ 1: Chứng minh bất đẳng thức cơ bản
Cho \( a = 3 \), \( b = 4 \), \( p = 2 \), và \( q = 2 \). Chứng minh rằng:
$ab \leq \frac{a^2}{2} + \frac{b^2}{2}.$
Giải
Tích \( ab = 3 \cdot 4 = 12 \).
Vế phải: $\frac{a^2}{2} + \frac{b^2}{2} = \frac{3^2}{2} + \frac{4^2}{2} = \frac{9}{2} + \frac{16}{2} = \frac{25}{2} = 12.5.$
Do đó, \( ab \leq \frac{a^2}{2} + \frac{b^2}{2} \), bất đẳng thức đúng.
Bất đẳng thức Young là một công cụ quan trọng trong toán học, với sự liên hệ chặt chẽ đến các bất đẳng thức cơ bản khác như Holder, Minkowski, và AM-GM. Với phạm vi ứng dụng rộng trong giải tích, tối ưu hóa, và vật lý, bất đẳng thức Young không chỉ là một kết quả lý thuyết mà còn mang lại nhiều giá trị thực tiễn. Việc hiểu rõ và vận dụng bất đẳng thức này sẽ giúp chúng ta giải quyết hiệu quả các bài toán phức tạp trong toán học và các ngành khoa học khác.