Bất đẳng thức Jensen

Là một trong những bất đẳng thức quan trọng và cơ bản trong toán học, đặc biệt trong lý thuyết hàm lồi. Được đặt theo tên nhà toán học người Đan Mạch Johan Jensen, bất đẳng thức này là một công cụ mạnh mẽ để phân tích các hàm lồi và lõm, đồng thời có ứng dụng rộng rãi trong xác suất, thống kê, lý thuyết thông tin và nhiều lĩnh vực khác.

Trong bài viết này, chúng ta sẽ tìm hiểu khái niệm bất đẳng thức Jensen, cách phát biểu chính xác, chứng minh, ý nghĩa toán học, cùng với một số ví dụ minh họa và ứng dụng thực tiễn.

1. Định nghĩa hàm lồi và hàm lõm

Trước khi đi sâu vào bất đẳng thức Jensen, chúng ta cần hiểu khái niệm về hàm lồi và hàm lõm, vì đây là nền tảng lý thuyết quan trọng.

Hàm lồi: Một hàm số \(f : I \to \mathbb{R}\) (với \(I\) là một khoảng trên tập số thực) được gọi là lồi nếu với mọi \(x_1, x_2 \in I\) và mọi \(t \in [0, 1]\), ta có: $f(tx_1 + (1 – t)x_2) \leq t f(x_1) + (1 – t) f(x_2).$

Hàm lõm: Một hàm số \(f : I \to \mathbb{R}\) được gọi là lõm nếu bất đẳng thức trên đảo ngược chiều: f(tx₁ + (1 – t)x₂) ≥ tf(x₁) + (1 – t)f(x₂).

Ý nghĩa hình học

• Nếu hàm \(f(x)\) là lồi, đồ thị của \(f\) nằm bên dưới hoặc trên đường thẳng nối hai điểm bất kỳ trên đồ thị.
• Nếu hàm \(f(x)\) là lõm, đồ thị của \(f\) nằm bên trên hoặc trên đường thẳng nối hai điểm bất kỳ trên đồ thị.

2. Phát biểu bất đẳng thức Jensen

Bất đẳng thức Jensen là một tính chất quan trọng của hàm lồi và hàm lõm. Nó mô tả mối quan hệ giữa giá trị của một hàm lồi (hoặc lõm) tại trung bình trọng số của các điểm và trung bình trọng số của các giá trị của hàm tại các điểm đó.

Phát biểu bất đẳng thức Jensen

Cho \(f : I \to \mathbb{R}\) là một hàm lồi trên khoảng \(I\), và cho \(x_1, x_2, \dots, x_n \in I\) cùng với các hệ số \(a_1, a_2, \dots, a_n\) thỏa mãn: $a_i \geq 0 \quad \text{và} \quad \sum_{i=1}^n a_i = 1,$

khi đó, bất đẳng thức Jensen được viết dưới dạng: $f\left( \sum_{i=1}^n a_i x_i \right) \leq \sum_{i=1}^n a_i f(x_i).$

Trường hợp hàm lõm

Nếu \(f(x)\) là hàm lõm, bất đẳng thức đảo chiều: $f\left( \sum_{i=1}^n a_i x_i \right) \geq \sum_{i=1}^n a_i f(x_i).$

Ý nghĩa

• Bất đẳng thức Jensen cho thấy rằng khi lấy giá trị của hàm lồi tại trung bình trọng số của các điểm \(x_i\), giá trị đó sẽ không lớn hơn trung bình trọng số các giá trị của hàm tại các điểm \(x_i\).
• Điều tương tự áp dụng cho hàm lõm, nhưng theo chiều ngược lại.

3. Chứng minh bất đẳng thức Jensen

Chứng minh trong trường hợp \(n = 2\)

Giả sử \(f(x)\) là hàm lồi trên khoảng \(I\), và \(a_1, a_2 \geq 0\) với \(a_1 + a_2 = 1\). Ta cần chứng minh: f(a₁x₁ + a₂x₂) ≤ a₁f(x₁) + a₂f(x₂).

Bởi vì \(f(x)\) là hàm lồi, theo định nghĩa, ta có:  f(tx₁ + (1–t)x₂) ≤ tf(x₁) + (1 – t)f(x₂),∀t ∈ [0, 1].

Đặt \(t = a_1\) và \(1 – t = a_2\), ta thu được: $f(a_1 x_1 + a_2 x_2) \leq a_1 f(x_1) + a_2 f(x_2).$

Chứng minh tổng quát cho \(n\) điểm

Cho \(f(x)\) là hàm lồi trên khoảng \(I\), và \(a_1, a_2, \dots, a_n \geq 0\) với \(\sum_{i=1}^n a_i = 1\). Ta cần chứng minh: $f\left( \sum_{i=1}^n a_i x_i \right) \leq \sum_{i=1}^n a_i f(x_i).$

Ta có thể chứng minh bất đẳng thức này bằng phương pháp quy nạp toán học trên \(n\):

• Cơ sở quy nạp (\(n = 2\)): Đã chứng minh ở phần trên.
• Bước quy nạp: Giả sử bất đẳng thức đúng với \(n = k\), tức là: $f\left( \sum_{i=1}^k a_i x_i \right) \leq \sum_{i=1}^k a_i f(x_i).$ Với \(n = k + 1\), ta có: $f\left( {\sum\limits_{i = 1}^{k + 1} {{a_i}} {x_i}} \right)$ = $f\left( {{a_{k + 1}}{x_{k + 1}} + \left( {1 – {a_{k + 1}}} \right)\sum\limits_{i = 1}^k {\frac{{{a_i}}}{{1 – {a_{k + 1}}}}} {x_i}} \right)$

Do tính chất lồi của \(f(x)\), áp dụng cho hai điểm \(x_{k+1}\) và \(\sum_{i=1}^k \frac{a_i}{1 – a_{k+1}} x_i\), ta có: $f\left( {\sum\limits_{i = 1}^{k + 1} {{a_i}} {x_i}} \right)$ $ \le $ ${a_{k + 1}}f({x_{k + 1}}) + (1 – {a_{k + 1}})f\left( {\sum\limits_{i = 1}^k {\frac{{{a_i}}}{{1 – {a_{k + 1}}}}} {x_i}} \right).$

Áp dụng giả thiết quy nạp cho phần còn lại, ta thu được bất đẳng thức Jensen tổng quát.

Một cách khác: Dùng bất đẳng thức Chebyshev để chứng minh

• Chọn \( a_i = f(x_i) \) và \( b_i = w_i \).
• Vì \( f \) là hàm lồi, dãy \( f(x_i) \) có cùng thứ tự tăng hoặc giảm với dãy \( x_i \).
• Khi đó, áp dụng bất đẳng thức Chebyshev ta có:

$\sum_{i=1}^{n} w_i f(x_i) \geq f \left( \sum_{i=1}^{n} w_i x_i \right) \sum_{i=1}^{n} w_i$

Vì \( \sum w_i = 1 \), ta suy ra: $\sum_{i=1}^{n} w_i f(x_i) \geq f \left( \sum_{i=1}^{n} w_i x_i \right)$

Vậy ta đã chứng minh được bất đẳng thức Jensen bằng bất đẳng thức Chebyshev.

4. Bài tập minh họa

Bài tập 1: Chứng minh với mọi ΔABC ta có: sinA +  sinB + sinC ≤ $\frac{{3\sqrt 3 }}{2}$

Giải

Xét f(x) = sinx với x ∈ (0; π) ⇒ f(x) là hàm lồi.

Theo bdt Jensen ta có: f(A) + f(B) + f(C) $ \le 3f\left( {\frac{{A + B + C}}{3}} \right)$ $ = 3\sin \left( {\frac{\pi }{3}} \right)$ $ = \frac{{3\sqrt 3 }}{2}\left( {dpcm} \right)$

Đẳng thức xảy ra khi chi khi ΔABC đều.

Bài tập 2: Chứng minh với mọi ΔABC đều ta có: $\tan \left( {\frac{A}{2}} \right) + \tan \left( {\frac{B}{2}} \right) + \tan \left( {\frac{C}{2}} \right) \ge \sqrt 3 $

Lời giải

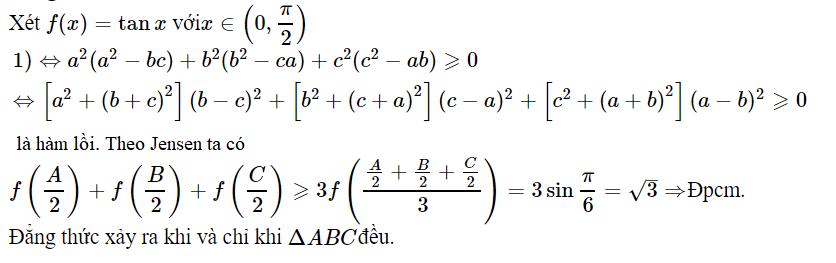
Bài tập 3: Chứng minh với mọi ΔABC đều ta có:

$\sin \left( {\frac{A}{2}} \right)$ + $\sin \left( {\frac{B}{2}} \right)$ + $\sin \left( {\frac{C}{2}} \right)$ + $\tan \left( {\frac{A}{2}} \right)$ + $\tan \left( {\frac{B}{2}} \right)$ + $\tan \left( {\frac{C}{2}} \right)$ $ \ge \frac{3}{2} + \sqrt 3 $

Lời giải

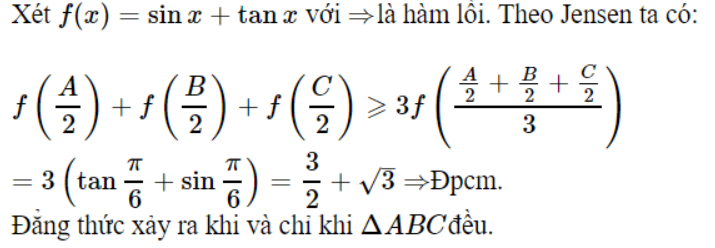
Bài tập 4. Chứng minh rằng với mọi ∆ABC ta có: ${\left( {\tan \frac{A}{2}} \right)^{2\sqrt 2 }} + {\left( {\tan \frac{B}{2}} \right)^{2\sqrt 2 }} + {\left( {\tan \frac{C}{2}} \right)^{2\sqrt 2 }} \ge {3^{1 – \sqrt 2 }}$

Lời giải

Xét $f\left( x \right) = {\left( {\tan x} \right)^{2\sqrt 2 }}$

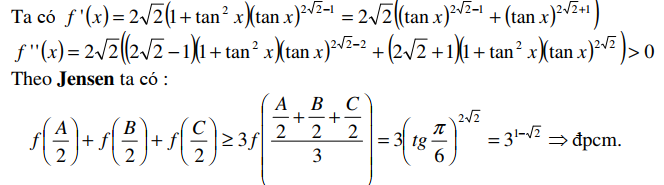
Dấu bằng xảy ra khi và chỉ khi ∆ABC là đều.

Bài tập 5: Trung bình cộng và trung bình nhân

Xét hàm lồi \(f(x) = \ln(x)\) trên khoảng \((0, \infty)\). Theo bất đẳng thức Jensen, với các số dương \(x_1, x_2, \dots, x_n\) và trọng số \(a_1, a_2, \dots, a_n \geq 0\) (thỏa mãn \(\sum a_i = 1\)), ta có: $\ln\left( \sum_{i=1}^n a_i x_i \right) \leq \sum_{i=1}^n a_i \ln(x_i).$

Lấy mũ hai vế, ta thu được: $\prod_{i=1}^n x_i^{a_i} \leq \sum_{i=1}^n a_i x_i.$

Đây chính là bất đẳng thức giữa trung bình cộng và trung bình nhân.

Bài tập 6: Tính giá trị kỳ vọng

Trong xác suất, bất đẳng thức Jensen khẳng định rằng nếu \(f(x)\) là hàm lồi và \(X\) là một biến ngẫu nhiên, thì: $f(\mathbb{E}[X]) \leq \mathbb{E}[f(X)].$

Ví dụ, nếu \(f(x) = x^2\), ta có: $(\mathbb{E}[X])^2 \leq \mathbb{E}[X^2].$

Điều này được sử dụng rộng rãi trong thống kê và lý thuyết thông tin.

Bài tập 7: Giả sử các số thực x1, x2,…, xn có tổng bằng 1. Chứng minh: $\frac{{{x_1}}}{{\sqrt {1 – {x_1}} }} + \frac{{{x_2}}}{{\sqrt {1 – {x_2}} }} + … + \frac{{{x_n}}}{{\sqrt {1 – {x_n}} }} \ge \sqrt {\frac{n}{{n – 1}}} $

Lời giải

Ta dễ chứng minh được f(x) là hàm lồi với $f\left( x \right) = \frac{x}{{\sqrt {1 – x} }},\,x \in \left( {0;\,1} \right)$

Và do đó áp dụng bất đẳng thức Jensen ta có điều phải chứng minh

Bài tập 8. Chứng minh rằng với mọi ∆ABC nhọn ta có: ${\left( {\sin A} \right)^{\sin A}}.{\left( {\sin B} \right)^{\sin B}}.{\left( {\sin C} \right)^{\sin C}} \ge {\left( {\frac{2}{3}} \right)^{\frac{{3\sqrt 3 }}{2}}}$

Lời giải

5. Ứng dụng của bất đẳng thức Jensen

BĐT Jensen là công cụ mạnh mẽ để chứng minh những bất đẳng thức kinh điển thường gặp như bất đẳng thức Cauchy, bất đẳng thức Bunhiacopxki, bất đẳng thức Holder, Bất đẳng thức Mincopxki, bất đẳng thức Karamata, bđt Sacno, bđt Petrovica, bđt Vasic, bđt  Young và Bất đẳng thức liên hệ giữa trung bình cộng, trung bình nhân, trung bình toàn phương và trung bình điều hòa.

Ngoài ra, bất đẳng thức Jensen có rất nhiều ứng dụng trong các lĩnh vực khác nhau:

• Xác suất và thống kê: Dùng để phân tích kỳ vọng, phương sai, và các tính chất của biến ngẫu nhiên.
• Lý thuyết thông tin: Sử dụng để chứng minh các tính chất của entropy và các đại lượng liên quan.
• Tối ưu hóa: Áp dụng trong bài toán tối ưu hóa liên quan đến hàm lồi.
• Tài chính: Dùng để phân tích rủi ro và lợi nhuận trong các mô hình tài chính.

6. Các tài liệu tham khảo

• Một số vấn đề về bất đẳng thức Jensen và ứng dụng
• Tài liệu về bất đẳng thức khác

7. FAQs

1. Bất đẳng thức Jensen là gì?

Bất đẳng thức Jensen phát biểu rằng nếu (f) là một hàm lồi và (\alpha_i \ge 0) với \(\sum \alpha_i = 1\), thì: $f!\left(\sum \alpha_i x_i\right) \le \sum \alpha_i f(x_i).$

2. Ai là người đưa ra bất đẳng thức Jensen?

Nó được đặt theo tên nhà toán học người Đan Mạch Johan Jensen.

3. Bất đẳng thức Jensen có áp dụng cho hàm lõm không?

Có, với hàm lõm, chiều bất đẳng thức sẽ đảo ngược.

4. Khi nào xảy ra dấu bằng trong bất đẳng thức Jensen?

Khi tất cả (x_i) bằng nhau hoặc khi hàm (f) là tuyến tính trên miền xét.

5. Bất đẳng thức Jensen thường được dùng trong lĩnh vực nào?

Nó được dùng rộng rãi trong xác suất, thống kê, giải tích và lý thuyết thông tin.

6. Có dạng tích phân của bất đẳng thức Jensen không?

Có, bất đẳng thức Jensen có thể mở rộng cho tích phân với trọng số.

7. Bất đẳng thức Jensen có vai trò gì trong xác suất?

Nó giúp đánh giá kỳ vọng của hàm ngẫu nhiên: $f(\mathbb{E}[X]) \le \mathbb{E}[f(X)].$

8. Jensen có được giảng dạy trong chương trình phổ thông không?

Không phổ biến trong phổ thông, nhưng xuất hiện nhiều trong chương trình đại học và tài liệu toán nâng cao.

9. Bất đẳng thức Jensen có liên hệ gì với hàm lồi?

Đây chính là bất đẳng thức đặc trưng cho định nghĩa hàm lồi.

10. Có thể áp dụng Jensen cho dãy vô hạn không?

Có, miễn là tổng trọng số hội tụ về 1 và các giá trị hữu hạn.

11. Jensen có ứng dụng trong lý thuyết thông tin không?

Có, nó là cơ sở để chứng minh tính lồi của entropy và bất đẳng thức liên quan đến Kullback–Leibler divergence.

12. Có ứng dụng nào của Jensen trong học máy (machine learning) không?

Có, bất đẳng thức Jensen thường được dùng để thiết lập giới hạn cho các hàm mất mát và thuật toán tối ưu.

13. Jensen có thể áp dụng trong bất đẳng thức lượng giác không?

Có, khi coi các hàm lượng giác như \(\sin, \cos, \ln, e^x\) là hàm lồi hoặc lõm trên miền xác định.

14. Bất đẳng thức Jensen có vai trò gì trong phân phối xác suất?

Nó giúp đánh giá các đặc trưng trung tâm như trung bình, phương sai thông qua hàm lồi.

15. Jensen có áp dụng được cho số phức không?

Thường chỉ xét cho số thực, nhưng có mở rộng trong một số bối cảnh đặc biệt của giải tích phức.

16. Có dạng rời rạc của bất đẳng thức Jensen không?

Có, chính là dạng tổng hữu hạn với trọng số \(\alpha_i\).

17. Bất đẳng thức Jensen có ứng dụng trong giải tích hàm không?

Có, nó được dùng để nghiên cứu tính lồi của chuẩn và toán tử.

18. Có chứng minh trực quan nào cho Jensen không?

Có, thường qua hình học: đồ thị hàm lồi luôn nằm phía trên đoạn thẳng nối hai điểm trên đồ thị.

19. Jensen có thể dùng trong bất đẳng thức tích phân không?

Có, nó thường giúp ước lượng giá trị trung bình của hàm tích phân.

20. Bất đẳng thức Jensen có mở rộng cho đa biến không?

Có, Jensen áp dụng cho nhiều biến cùng lúc với trọng số thích hợp.

21. Vì sao bất đẳng thức Jensen quan trọng?

Vì nó là cầu nối giữa lý thuyết hàm lồi và các ứng dụng thực tiễn trong toán học, thống kê, kinh tế và khoa học dữ liệu.

8. Kết luận

Bất đẳng thức Jensen là một công cụ mạnh mẽ và linh hoạt trong toán học, đặc biệt trong phân tích các hàm lồi và lõm. Nó không chỉ cung cấp một cái nhìn sâu sắc về tính chất của hàm lồi mà còn đóng vai trò quan trọng trong nhiều lĩnh vực như xác suất, thống kê, tối ưu hóa và lý thuyết thông tin. Với sự tổng quát và ứng dụng rộng rãi, bất đẳng thức Jensen thực sự là một trong những bất đẳng thức nổi bật trong toán học hiện đại.