Bất đẳng thức Cosi (Cauchy) chi tiết nhất 2025

Trong toán học, một trong những bất đẳng thức nổi bật là bất đẳng thức Cosi (Cauchy-Schwarz), một công cụ mạnh mẽ trong nhiều lĩnh vực như đại số tuyến tính, giải tích, và lý thuyết số. Bất đẳng thức này không chỉ có ứng dụng lý thuyết mà còn được ứng dụng rộng rãi trong các bài toán thực tiễn.

Bất đẳng thức Cosi cho hai số là một trường hợp đặc biệt, cho phép chúng ta so sánh kích thước của các số trong không gian Euclid. Bài viết này sẽ đi sâu vào việc khám phá bất đẳng thức Cosi với hai số, từ định nghĩa cho đến ứng dụng và ví dụ minh họa.

1. Định nghĩa

Cho \(a_1, a_2, \dots, a_n\) và \(b_1, b_2, \dots, b_n\) là các số thực hoặc số phức, ta có:

$\left( \sum_{i=1}^n a_i b_i \right)^2 \leq \left( \sum_{i=1}^n a_i^2 \right) \left( \sum_{i=1}^n b_i^2 \right),$

dấu “=” xảy ra khi và chỉ khi tồn tại hằng số \(k\) sao cho \(a_i = k b_i\) với mọi \(i\).

Dạng trung bình cộng và trung bình nhân:

Một hệ quả quan trọng của bất đẳng thức này là: $\frac{a_1 + a_2 + \dots + a_n}{n} \geq \sqrt[n]{a_1 \cdot a_2 \cdot \dots \cdot a_n},$
với dấu “=” xảy ra khi \(a_1 = a_2 = \dots = a_n\).

1.1 Hai số không âm

Bất đẳng thức Cô-si với hai số thực a và b được phát biểu như sau

Với mọi số thực a và b, ta có:

$\left( {{a^2} + {b^2}} \right) \ge \frac{{{{\left( {a + b} \right)}^2}}}{2}$

Dấu “=” xảy ra nếu và chỉ nếu a = b.

Nội dung: Bất đẳng thức này cho thấy rằng tổng bình phương của hai số luôn lớn hơn hoặc bằng bình phương của tổng các số đó, chia cho 2.

Bất đẳng thức này có thể được hiểu rằng trung bình cộng của bình phương hai số a² và b² luôn lớn hơn hoặc bằng bình phương trung bình nhân của chúng $\sqrt {ab} $. Đây là một trường hợp đặc biệt của bất đẳng thức trung bình cộng lớn hơn hoặc bằng trung bình nhân (AM-GM).

1.2 Bất đẳng thức cosi cho 3 số không âm

\[ \frac{a + b + c } {3} \ge \sqrt [3] {abc} \]

Dấu bằng xảy ra khi và chỉ khi a = b = c

1.3 Bất đẳng thức cosi cho 4 số không âm

\[ \frac{a + b + c + d } {4} \ge \sqrt [4] {abcd} \]

Dấu bằng xảy ra khi và chỉ khi a = b = c = d

1.4 Bất đẳng thức cosi cho n số không âm

Với x₁, x₂,…, x_n là n số thực không âm, khi đó ta có:

\[ \frac{x_1+ x_2 + …, + x_n} {n} \ge \sqrt [n] {x_1x_2…x_n} \]

Đẳng thức xảy ra khi và chỉ khi x₁ = x₂ =… = x_n

2. Chứng minh bất đẳng thức Cosi

Xét hiệu số giữa trung bình cộng và trung bình nhân:

$\frac{{{a^2} + {b^2}}}{2} – \sqrt {a.b} $

Khai triển và biến đổi biểu thức này: $\frac{{{a^2} + {b^2}}}{2} – \sqrt {a.b} $ $ = \frac{{{a^2} + {b^2}}}{2} – \frac{{2\sqrt {a.b} }}{2}$ $ = \frac{{{a^2} + {b^2} – 2\sqrt {a.b} }}{2}$ $ = \frac{{{a^2} – 2\sqrt {a.b} + {b^2}}}{2}$ $ = \frac{{{{\left( {\sqrt a } \right)}^2} – 2\sqrt {a.b} + {{\left( {\sqrt b } \right)}^2}}}{2}$ $ = \frac{{{{\left( {\sqrt a – \sqrt b } \right)}^2}}}{2} \ge 0$

Vậy là: $\frac{{{a^2} + {b^2}}}{2} – \sqrt {a.b} = \frac{{{{\left( {\sqrt a – \sqrt b } \right)}^2}}}{2} \ge 0$

Biểu thức này luôn không âm, vì bình phương của một số thực luôn không âm. Biểu thức này luôn không âm, vì bình phương của một số thực luôn không âm ${\left( {\sqrt a – \sqrt b } \right)^2} = 0$ $ \Rightarrow \sqrt a = \sqrt b $ $ \Rightarrow a = b$

Mở rộng:

• Bất đẳng thức Cauchy cho 3 số không âm: Cho a, b, c  ≥ 0. Khi đó: $\frac{{a + b + c}}{3} \ge \sqrt[3]{{abc}}$. Đẳng thức xảy ra ⇔ a = b = c
• Bất đẳng thức Cauchy cho n số không âm: Cho a₁, a₂, …, a_n ≥ 0. Khi đó: $\frac{{{a_1} + {a_2} + … + {a_n}}}{n} \ge \sqrt[n]{{{a_1}.{a_2}… + {a_n}}}$. Đẳng thức xảy ra ⇔ a₁ = a₂ = … = a_n

Sử dụng BĐT Jensen chứng minh BĐT cosi

Hệ quả quan trọng

• Hệ quả 1: Với a, b > 0 thì $\frac{1}{a} + \frac{1}{b} \ge \frac{4}{{a + b}}.$ Đẳng thức xảy ra ⇔ a = b
• Hệ quả 2: Với a, b, c > 0 thì $\frac{1}{a} + \frac{1}{b} + \frac{1}{c} \ge \frac{9}{{a + b + c}}.$ Đẳng thức xảy ra ⇔ a = b = c
• Hệ quả 3: Cho n số thực dương a₁, a₂, …, a_n. Khi đó $\sqrt[n]{{{a_1}.{a_2}….{a_n}}} \ge \frac{n}{{\frac{1}{{{a_1}}} + \frac{1}{{{a_2}}} + … + \frac{1}{{{a_n}}}}}$. Đẳng thức xảy ra ⇔ a₁ = a₂ = … = a_n
• Hệ quả 4: Cho a, b ≥ 0 và m, n ∈ ℕ. Khi đó a^{m + n} + b^{m + n} ≥ a^mbⁿ + aⁿb^m. Đẳng thức xảy ra ⇔ a = b

Dạng đặc biệt của bất đẳng thức cosi cần nhớ:

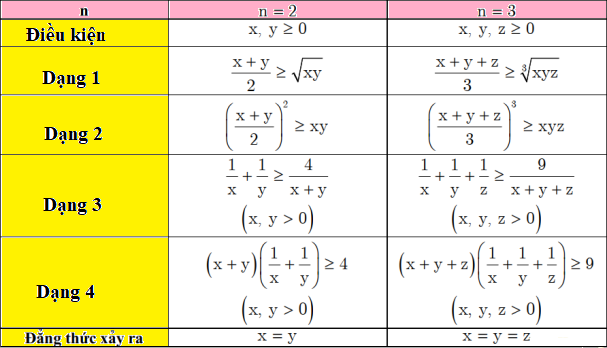
3. Các dạng bài tập

Bài tập 1: Chứng minh rằng: $a^2 + b^2 \geq 2ab$

Lời giải

Đây là một trường hợp đặc biệt của bất đẳng thức Cô-si. Ta có:

$a^2 + b^2 – 2ab = (a – b)^2 \geq 0$

Dấu “=” xảy ra khi \(a = b\).

Bài tập 2: Tìm giá trị lớn nhất của y = x²(1 – x), x ∈ (0, 1)

Lời giải

Do x, 1 – x > 0 nên áp dụng bất đẳng thức Cauchy ta có:

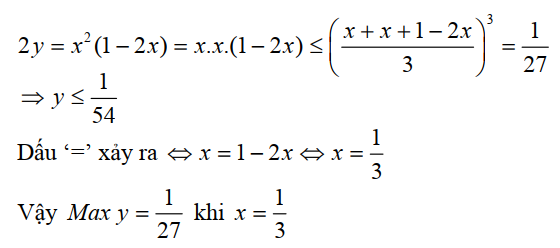
Bài tập 3: Cho a, b, c > 0. Chứng minh: ${a^2} + {b^2} + 4 \ge 2a + 2b + ab$

Lời giải

Áp dụng bất đẳng thức Cauchy với 2 số:

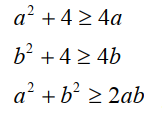
Cộng lại ta được: 2a² + 2b² + 8 ≥ 4a + 4b + 2ab (đpcm)

Dấu ‘=’ xảy ra khi chỉ khi a = b = 2

Bài tập 4: Cho a, b, c > 0. Chứng Minh ${a^3} + {b^3} + {c^3} \ge {a^2}.\sqrt {bc} + {b^2}.\sqrt {ac} + {c^2}.\sqrt {ab} $

Lời giải

Áp dụng Cauchy 6 số:

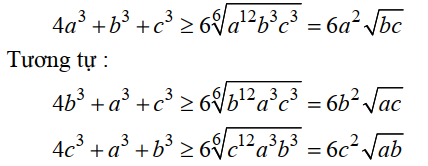
Cộng các vế lại ta được điều phải chứng minh.

Dấu ‘=’ xảy ra khi chỉ khi a = b = c

Bài tập 5: Cho a, b, c > 0. Chứng minh

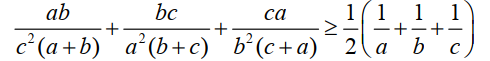
Lời giải

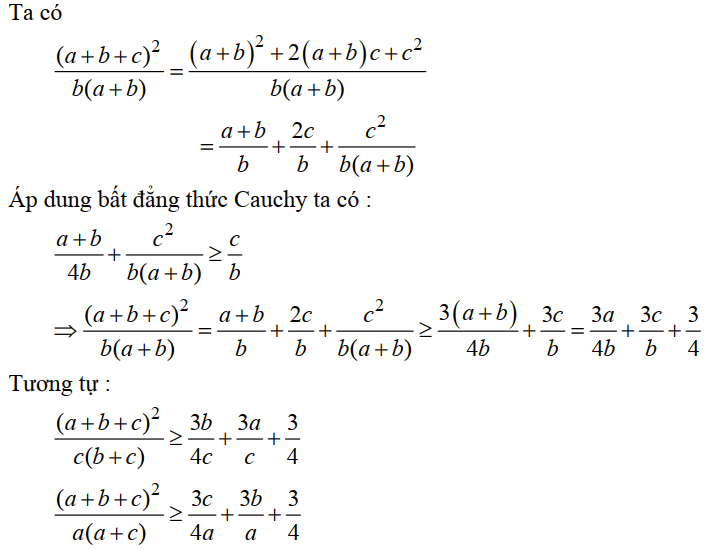
Cộng các vế lại và áp dụng bất đẳng thức Cô-si ta được đpcm

Bài tập 6: Cho \(a, b > 0\). Chứng minh rằng: $\frac{a^2 + b^2}{2} \geq \sqrt{a \cdot b}$

Lời giải

Từ bất đẳng thức AM-GM, ta có: $\frac{a^2 + b^2}{2} \geq \sqrt{a^2 \cdot b^2} = \sqrt{a \cdot b}.$

Dấu “=” xảy ra khi \(a = b\).

Bài tập 7: Tìm giá trị nhỏ nhất của biểu thức: $P = \frac{x^2 + y^2}{2xy}$ với \(x, y > 0\).

Lời giải

Sử dụng bất đẳng thức Cô-si: $\frac{x^2 + y^2}{2} \geq \sqrt{x \cdot y} \Rightarrow P \geq 1.$

Dấu “=” xảy ra khi \(x = y\). Do đó, giá trị nhỏ nhất của \(P\) là 1.

Bài 8: Chứng minh với mọi x, y, z dương

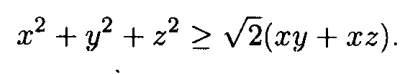
Lời giải

Ta thấy: ${x^2} + {y^2} + {z^2} \ge {x^2} + \frac{{{y^2} + {z^2}}}{2}$

Sử dụng bất đẳng thức AM – GM với 2 số:

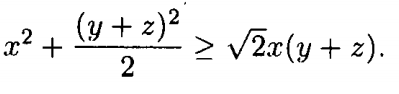
Từ 2 biểu thức trên, ta suy ra:

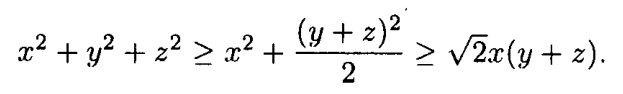
Điều cần phải chứng minh.

Bài 9: Chứng minh với mọi số thực dương a, b, c, d ta luôn có:

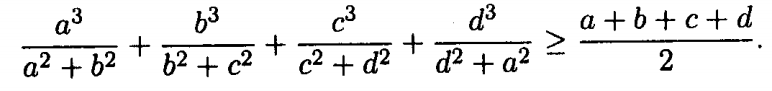
Lời giải

Sử dụng bất đẳng thức AM – GM với 2 số:

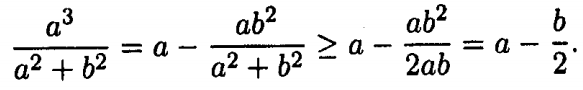
Xây dựng 3 bất đẳng thức tương tự với b, c, d rồi cộng vế các bất đẳng thức lại ta có điêu phải chứng minh. Đẳng thức xảy ra khi tất cả các biến bằng nhau.

Bài 10: Cho a, b, c ≥ 0 và a + b + c = 3. Chứng minh rằng

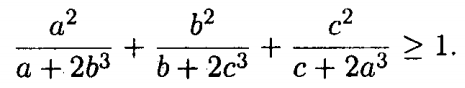
Lời giải

Chứng minh tương tư, đưa bất đẳng thức về $b\sqrt[3]{{{a^2}}} + c\sqrt[3]{{{b^2}}} + a\sqrt[3]{{{c^2}}} \le 3$

Sau đó áp dụng bất đẳng thức AM – GM:

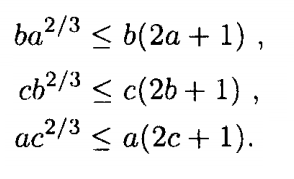
Cộng vế cả 3 bất đẳng thức trên ta có điều phải chứng minh.

4. Ứng dụng của bất đẳng thức Cauchy-Schwarz (Cô-si)

Ý nghĩa toán học: Bất đẳng thức Cô-si với hai số là một phần của bất đẳng thức trung bình cộng và trung bình nhân, đặt nền tảng cho nhiều lĩnh vực trong toán học như:

• Đại số: Tìm giá trị lớn nhất/nhỏ nhất của biểu thức và ứng dụng trong việc giải phương trình, bất phương trình.
• Hình học: Chứng minh bất đẳng thức liên quan đến tam giác (bán kính đường tròn nội tiếp, ngoại tiếp, diện tích). Ngoài ra còn dùng để thiết lập các tính chất về khoảng cách và tọa độ.
• Giải tích: Giúp tìm giá trị lớn nhất hoặc nhỏ nhất của các biểu thức.
• Trong lý thuyết số và tổ hợp: Ứng dụng trong bài toán đếm số cách phân chia.

Ứng dụng trong thực tế: Trong thực tế, bất đẳng thức Cô-si giúp chúng ta hiểu rằng sự cân bằng giữa các yếu tố thường mang lại hiệu quả tối ưu. Ví dụ:

• Sản xuất: Nếu a và b đại diện cho năng suất của hai máy móc, bất đẳng thức Cô-si cho thấy việc cân bằng năng suất giữa hai máy sẽ hiệu quả hơn so với việc một máy làm việc quá tải còn máy kia thì hoạt động ít.
• Tài chính: Trong đầu tư, bất đẳng thức này có thể được sử dụng để tối ưu hóa lợi nhuận khi phân bổ nguồn lực.

5. Mối liên hệ giữa bất đẳng thức Cô-si và các bất đẳng thức khác

• Bất đẳng thức Minkowski: Mở rộng Cô-si cho tổng n số.
• Bất đẳng thức Holder: Tổng quát hóa bất đẳng thức Cô-si trong không gian L^P.
• Bất đẳng thức Jensen: Liên hệ với các hàm lồi trong giải tích.

6. Kinh nghiệm khi sử dụng bất đẳng thức Cô-si

Bất đẳng thức Cô-si là một trong những công cụ mạnh mẽ và phổ biến trong toán học, được áp dụng rộng rãi trong nhiều lĩnh vực, từ đại số đến giải tích và hình học. Tuy nhiên, việc sử dụng hiệu quả bất đẳng thức này đòi hỏi sự tinh tế, hiểu biết sâu sắc và kinh nghiệm thực tiễn. Trong bài viết này, chúng ta sẽ cùng tìm hiểu ba khía cạnh quan trọng để vận dụng bất đẳng thức Cô-si một cách tối ưu: khi nào nên sử dụng, những sai lầm phổ biến và mẹo để nhận diện dạng bài toán phù hợp.

6.1 Khi nào nên chọn bất đẳng thức Cô-si?

Bất đẳng thức Cô-si thường được áp dụng trong các bài toán liên quan đến:

• Biểu thức có dạng tổng hoặc tích bình phương: Ví dụ, khi gặp các biểu thức dạng a² + b² hoặc (a+b)², bất đẳng thức Cô-si có thể giúp chuyển đổi biểu thức thành dạng dễ xử lý hơn.
• Bài toán tối ưu hóa: Bất đẳng thức này rất hữu ích trong việc tìm giá trị lớn nhất hoặc nhỏ nhất của một biểu thức. Đặc biệt, nó thường xuất hiện trong các bài toán tìm cực trị của hàm số hoặc biểu thức đại số.
• Các bài toán đòi hỏi ước lượng: Khi cần đánh giá một biểu thức phức tạp hoặc thiết lập mối quan hệ giữa các đại lượng, bất đẳng thức Cô-si cung cấp cách ước lượng hiệu quả mà không cần tính toán chi tiết.

6.2 Những sai lầm phổ biến khi áp dụng bất đẳng thức Cô-si

Dù mạnh mẽ và hữu ích, bất đẳng thức Cô-si cũng dễ dẫn đến sai lầm nếu không được áp dụng đúng cách. Một số lỗi phổ biến bao gồm:

• Không kiểm tra điều kiện áp dụng: Bất đẳng thức Cô-si yêu cầu các số hạng tham gia phải là số thực (hoặc không âm trong một số trường hợp). Nhiều học sinh thường bỏ qua bước kiểm tra này, dẫn đến kết quả sai.
• Nhầm lẫn dạng áp dụng: Bất đẳng thức Cô-si có nhiều biến thể (tích phân, vector, tổng quát hóa, v.v.), việc áp dụng sai biến thể sẽ làm sai lệch kết quả. Ví dụ, nhầm lẫn giữa dạng (a+b)² và dạng tổng quát a₁b₁+a₂b₂+⋯+a_nb_n.
• Bỏ qua khả năng đơn giản hóa bài toán: Một số trường hợp, bất đẳng thức AM-GM hoặc các phương pháp khác có thể hiệu quả hơn Cô-si, nhưng người giải thường cố áp dụng Cô-si một cách máy móc, làm bài toán phức tạp hơn.

6.3 Mẹo để nhận diện dạng bài toán phù hợp với bất đẳng thức Cô-si

Nhận diện nhanh bài toán phù hợp với bất đẳng thức Cô-si là kỹ năng cần thiết. Dưới đây là một số mẹo giúp bạn:

• Tìm dấu hiệu quen thuộc: Hãy chú ý đến các biểu thức chứa tổng bình phương hoặc tích vô hướng. Đây thường là dấu hiệu bài toán có thể giải bằng Cô-si.
• Phân tích vai trò các đại lượng: Nếu bài toán yêu cầu ước lượng giá trị của một tổng hoặc một tích, bất đẳng thức Cô-si có thể là lựa chọn đúng.
• So sánh với các bất đẳng thức khác: Đôi khi bài toán có thể giải được bằng nhiều cách, như AM-GM hoặc Bunyakovsky. Trong trường hợp này, hãy chọn bất đẳng thức Cô-si nếu bài toán liên quan đến nhiều biến và cần sự tổng quát.

7. Tài liệu tham khảo và mở rộng

Dưới đây là những tài liệu mà chúng tôi chia sẻ giúp bạn đọc có thêm tư liệu nghiên cứu bdt cosi này:

• Bảng tra cứu bất đẳng thức thường gặp
• Bài tập bất đẳng thức cauchy hay

Bạn có thể xem thêm các tài liệu khác tại đây.